作者SAMI PURMONEN

摘要 🔗

我们探索了蒙特卡洛树搜索（MCTS）和深度学习在预测Candy Crush游戏关卡难度（以成功尝试次数衡量）中的应用。通过大量的游戏玩家数据，我们训练了一个深度神经网络（DNN）来预测游戏状态的移动。该DNN在Candy Crush的大量关卡中游玩，然后我们拟合了一个回归模型来从机器人的难度中预测人类玩家的难度。我们将我们的结果与MCTS机器人的结果进行了对比。结果表明，DNN可以在明显较短的时间内，做出与MCTS相当的游戏关卡难度估计。

总结 🔗

我们探索了使用蒙特卡洛树搜索（MCTS）和深度学习来评估Candy Crush游戏关卡的难度。通过大量游戏数据，我们训练了一个深度神经网络（DNN）来预测从游戏关卡中的游戏动作。DNN在Candy Crush的各种关卡中进行游戏，我们构建了一个模型来预测从DNN难度中的人类玩家难度。我们将结果与MCTS进行了比较。我们的结果显示，DNN可以在显著较短的时间内做出与MCTS相当的评估。

致谢 🔗

我想感谢计算机科学与通信学院（CSC）的Karl Meinke教授对我的毕业论文的指导。我要感谢来自King公司AI团队的Stefan Freyr，Erik Poromaa和Alex Nodet，没有他们，这篇毕业论文的完成将无法成为可能。我还要对来自King公司AI团队的John Pertoft，Philipp Eisen和Lele Cao一直对我的工作提供反馈表示感谢。我要感谢Olov Engwall教授对我的论文的审阅。

第1章 🔗

引言 🔗

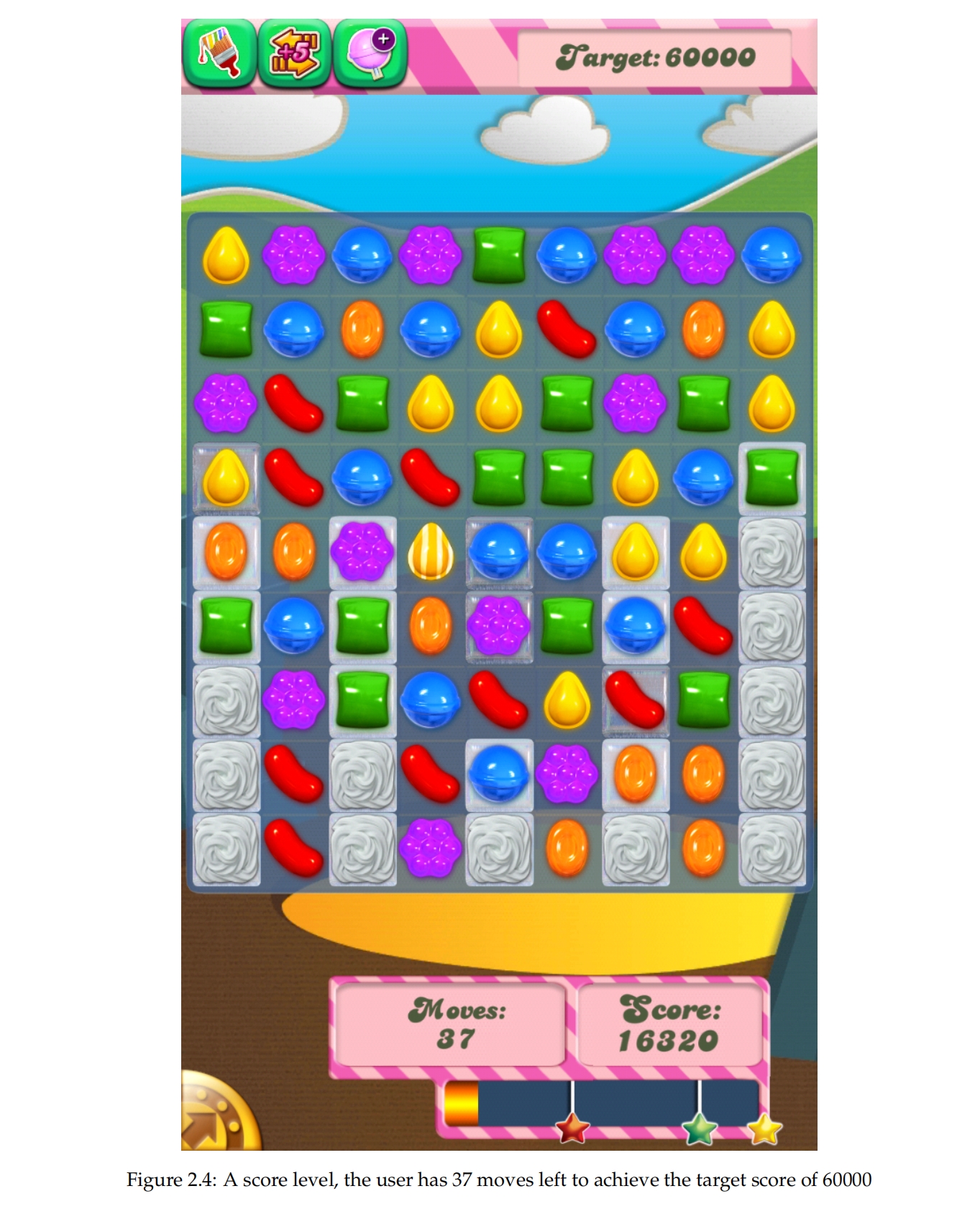
玩游戏可能很有趣，但前提是游戏的难度不能太难也不能太简单。如果游戏太难，玩家会感到沮丧并停止玩游戏。如果游戏太简单，玩家会感到无聊并停止玩游戏。在游戏发布给玩家之前，预测游戏关卡的难度是困难的。如果没有任何技术工具，关卡设计师只能多次手动玩关卡，然后根据对关卡设计师来说的难度，去猜测它对一般玩家的难度。然而，手动玩游戏需要大量时间，这导致在发布前的迭代次数较少。 对于游戏公司和关卡设计师来说，拥有能够快速并准确预测游戏关卡难度的工具将非常有用。这对于像King的Candy Crush这样不断发布新关卡的游戏尤其重要。它可以让关卡设计师在发布前多次调整关卡，以保证其难度适中。

1.1 机器人 🔗

预测游戏关卡难度的一种自动化方式是创建一个程序，一个机器人，按照某种策略来玩这个游戏。机器人可以多次玩一个关卡，并根据"每次成功所需的尝试次数"这样的难度度量标准，估计机器人觉得这个关卡有多难。如果我们让机器人玩很多关卡，然后估计每个关卡的机器人难度，我们可以比较这些难度与人类的难度，试图将机器人的难度与人类的难度关联起来。如果一关对人类来说相对困难，对机器人来说也相对困难；如果对人类来说相对容易，对机器人来说也相对容易，那么我们可能可以创建一个有效的回归模型，从机器人的难度中预测人类的难度。新关卡的难度可以通过让机器人多次玩这个关卡，测量机器人的难度，然后用预测模型从机器人的难度中预测人类的难度来预测。这样有很多种策略可以创建。

1.1.1 手动启发式 🔗

机器人可以使用的一种策略是手动启发式，这种策略会对可用的走法进行排名，然后选择最好的一种。这种启发式可以查看当前的游戏状态，以判断每个可用走法的吸引力。这种方法的缺点是它不具有通用性或可维护性。当游戏发生变化，例如引入新的游戏元素时，启发式需要进行更新。每个游戏都必须创建新的启发式。

1.1.2 蒙特卡洛树搜索 🔗

一种更通用的方法是蒙特卡洛树搜索（MCTS）。MCTS并不是创建一大套规则去决定一步走位的吸引力，而是使用仿真。MCTS会多次执行每一个走法，并试玩到最后，估计它通向成功的频率。这就不需要对游戏有任何知识，可以自动处理游戏改变的情况，或者被用在一个全新的游戏上。MCTS的缺点是它很慢，因为它需要模拟许多次游戏。

1.1.3 深度神经网络 🔗

机器学习也可以用来从游戏状态中对走法进行排序，本质上是从数据中学习启发式。如果一个包含有游戏状态和走法的大型数据集可用，那么就可以在监督学习中使用，来训练一个分类器，预测在任何给定的游戏状态中应选择哪种走法。深度神经网络（DNN）就是一种可用于分类的机器学习算法，并已在图像识别、机器翻译和游戏中取得了重大突破。使用DNN从游戏状态中预测走法将比MCTS快得多，因为它不需要进行模拟，同时也具有通用性，因为只需要新的数据集就能学习一个新的游戏。不解的问题是它是否也具有精确性。这就是本论文中將要探讨的问题。 表1.1显示了这些方法在假设上相互比较的情况。

1.2 问题 🔗

我们的研究问题是，在Candy Crush游戏中，使用深度神经网络（DNN）机器人是否可以比使用蒙特卡洛树搜索（MCTS）机器人更好地预测游戏关卡的难度。

1.3 界定范围 🔗

我们将研究范围限制在King的游戏Candy Crush，以及使用由MCTS机器人生成的训练数据。

第2章 🔗

相关理论 🔗

在本章中，我们提供我们工作基础的理论基础。我们深入研究了神经网络的工作原理和训练方式，因为这是本论文最重要的部分，也是工作的大部分投入时间所在。

2.1 相关工作 🔗

主要的灵感来源于谷歌DeepMind的AlphaGo论文和Erik Poromaas的硕士论文。其他的灵感来源于图像识别，因为从游戏状态预测着法的问题可以看作是一个图像识别问题。更广泛的灵感来源于与机器学习或游戏人工智能有关的任何内容。 在《利用深度神经网络和树搜索掌握围棋》中，发明了一款使用监督学习、强化学习和蒙特卡罗树搜索的计算机围棋程序。这是第一个能够在全尺寸棋盘上击败专业围棋选手的计算机围棋程序[1]。我们的工作受到AlphaGo的监督学习部分的启发，但我们将其用于预测游戏难度，而不是创建最强大的机器人。 在Candy Crush中，Erik Poromaa使用MCTS预测Candy Crush中的游戏水平难度。他发现这种方法优于先前的最先进的手动测试方法[2]。我们将我们的结果与他创建的MCTS机器人进行了比较。 在《利用深度卷积神经网络进行ImageNet分类》中，一个大型深度卷积神经网络在数百万高分辨率图像上进行训练，显著提高了以前在ImageNet LSVRC-2010比赛中的最新技术水平[3]。尽管这里的目标是确定图像中可见的对象类型，但与我们的问题类似，因为游戏棋盘可以被视为一个具有比RGB更多通道的图像，并且我们试图识别的对象是144个可能移动中的一个，因此卷积神经网络也适合我们的问题。 在《利用深度卷积神经网络在围棋中进行着法评估》中，一个12层的深度卷积神经网络在人类职业围棋选手的数据集上进行训练，用于预测着法。它以55%的准确率预测专业着法，并且可以击败传统的搜索程序而无需进行任何搜索[4]。这篇论文启发了AlphaGo，并与我们所做的非常相似，因为他们创建了一个基于仅监督学习的DNN机器人进行围棋比赛，然而我们进一步采取了一步，使用机器人来预测游戏难度。 在《使用卷积神经网络在国际象棋中预测着法》中，训练了一个深度卷积神经网络来预测国际象棋中的着法。国际象棋的问题在于一步着法由棋子移动的位置定义，因此需要一个分类器来区分64*64或4096种不同的着法。为了减少着法数量，他们采用了一种新颖的方法，创建了两个独立网络，一个用于预测移动哪个棋子，另一个用于预测在哪里移动它，从而将每个网络的类空间减少到64。他们成功以38.3%的准确率预测哪个棋子应该移动[5]。他们的目标是预测着法与我们的目标相同，只是我们不需要在减少类空间方面下一番苦功，因为我们问题中的着法数量是可管理的，而在围棋中有361种着法。 在《使用深度强化学习在Atari中玩游戏》中，创建了一个基于卷积神经网络和强化学习的模型来玩七款Atari 2600游戏。它在六款游戏中优于先前的所有方法，并在其中三款游戏中表现优于人类专家[6]。应用类似的强化方法到我们的问题可能会很有趣，但我们决定选择监督学习，因为我们认为预测游戏难度的最佳方法是创建一个模仿人类玩家的机器人。由于在本论文写作时我们没有人类玩家数据，因此无法实现这一目标，但可以在未来进行尝试。

2.2 蒙特卡洛树搜索 🔗

在创建玩游戏的代理程序时，通常会使用不同的游戏树搜索算法。极小化算法是一种树搜索算法，在棋类游戏如国际象棋、跳棋和奥赛洛中已经达到了最先进的性能，那里有用于评估游戏状态的良好启发式[1]。在围棋等很难提出启发式的游戏中，直到AlphaGo出现之前，MCTS一直是最成功的游戏搜索算法[4]。 MCTS通过使用随机抽样来扩展搜索树，从状态中确定最佳行动。它可应用于任何有限长度和有限移动次数的游戏。每个行动都是搜索树中的一个节点，并记录获胜次数和访问次数，这些数据用于引导搜索树朝着更好的走法发展。它由四个迭代执行的步骤组成：选择、扩展、模拟和回传，如图2.1所示。多次执行这些步骤会收敛到最佳的玩法[7]。

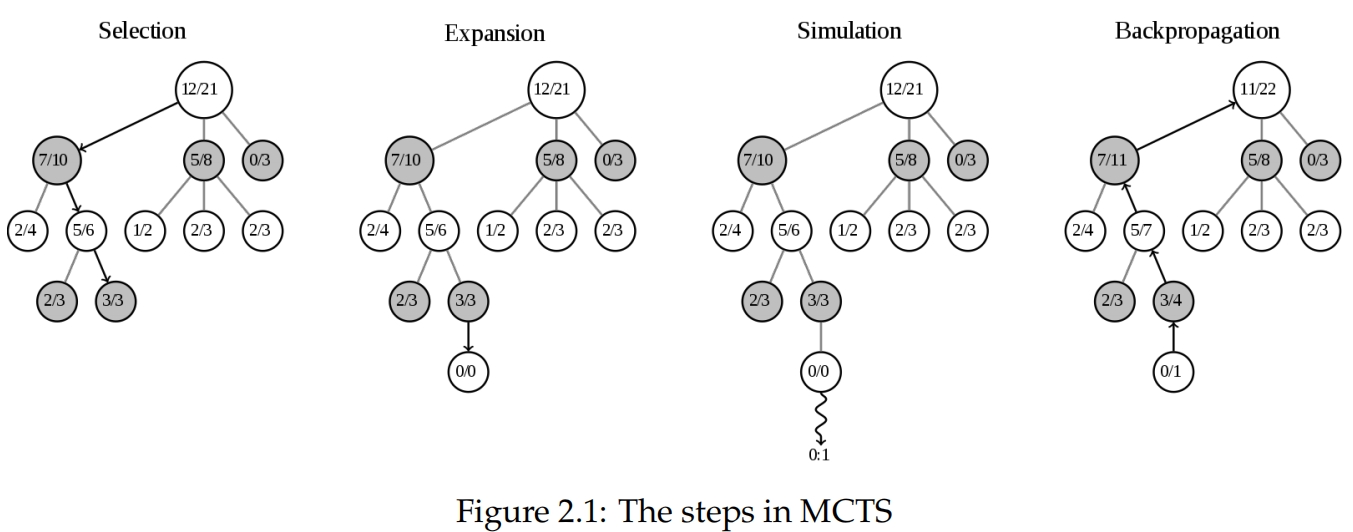
选择 选择从当前状态开始，也就是搜索树的根节点，然后选择子节点，直到达到叶子节点。选择子节点的方式是根据获胜次数和访问次数，但同时也允许探索，以便将树扩展为朝着最有希望的走法。 扩展 当到达叶子节点时，如果游戏尚未结束，则会向搜索树添加一个新的子节点。 模拟 通过随机选择行动对游戏进行模拟直到结束。 回传 游戏结果通过所有访问过的节点回传到根节点，更新获胜次数和访问次数。

2.3 机器学习 🔗

机器学习涵盖了从经验中学习的算法。监督学习是机器学习中最常见的形式。监督学习算法从这类映射的训练集示例中学习函数F：R^N → R^M，然后它在未见数据上的预测效果变得更好，这意味着它在泛化。

2.3.1 分类 🔗

分类意味着将有限类别集C中的类别c分配给输入特征。例如，我们可以有一个分类器，输入一个人的身高和体重，输出c ∈ {男性, 女性}。给定一组标记为女性或男性的人的体重和身高数据集，学习算法可以生成一个预测人们性别的分类器。分类器的目的是在未见数据上使用它，因此在训练期间的目标是训练一个泛化到未见数据的分类器。 数据表示 分类器的输入是一个向量X ∈ R^n，其中n是特征数量。分类器的输出是一个向量Y ∈ R^c，其中c是类别数量，Y_i是第i类的分数。预测的类别是arg max_i Y_i。Y可以被归一化，使得P i Y_i = 1，将其成为给定类别的条件概率分布P(i|X) = Y_i，使用softmax函数表示如2.1方程所示。

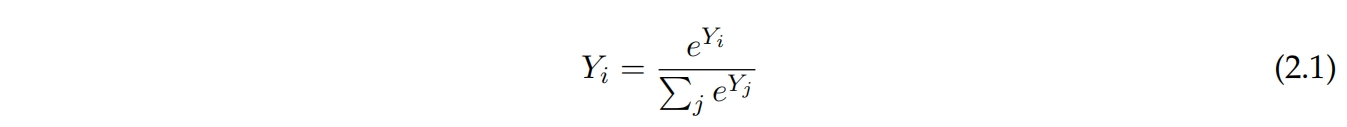
这是我们在本论文中对分类的看法。这是一种从输入向量生成所有可能类别的概率分布的方法。

2.3.2 人工神经网络 🔗

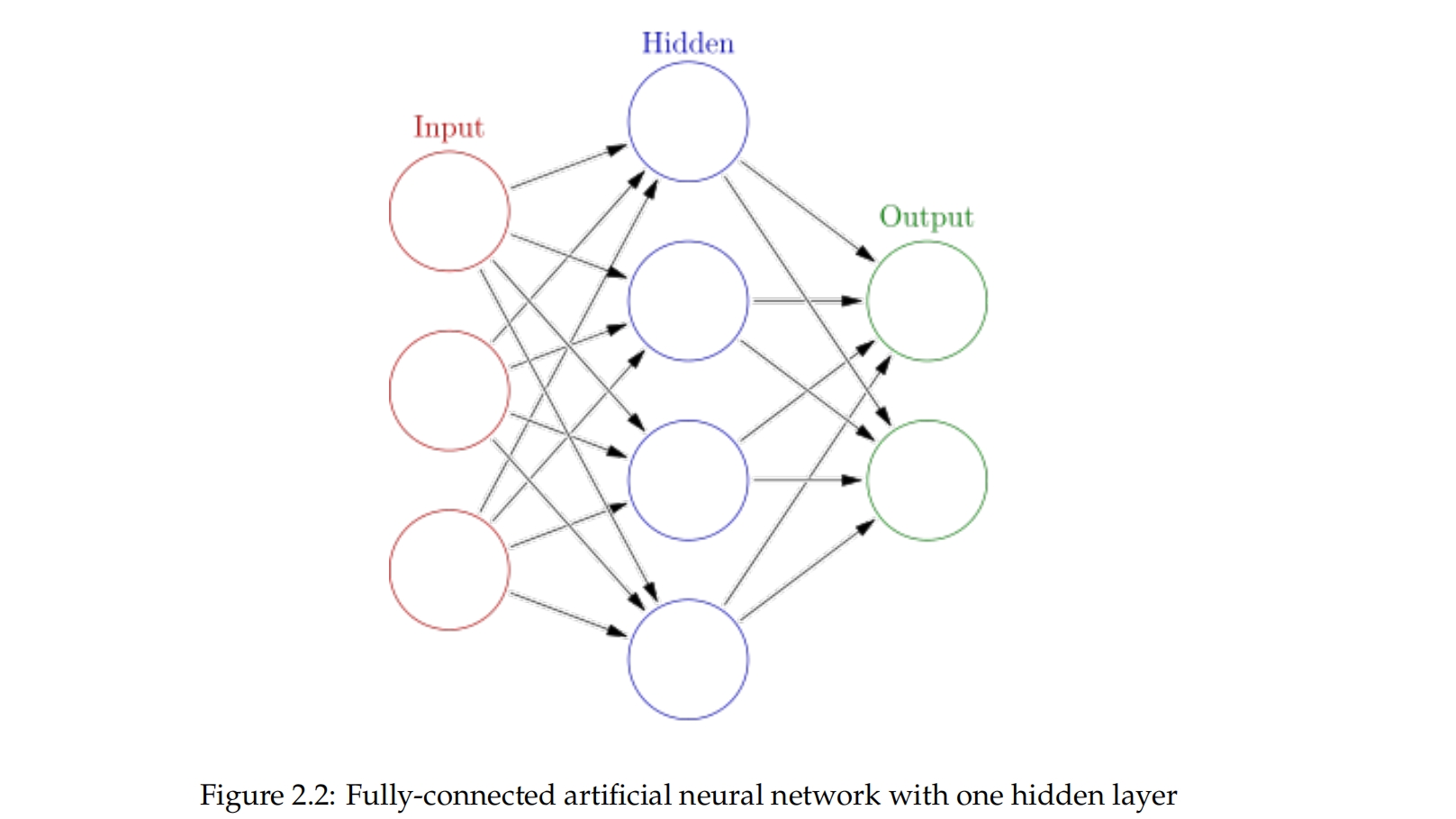
神经网络是一种监督学习算法。我们将讨论它如何用于分类任务。神经网络由相互连接的神经元层组成，具有权重。我们将讨论前馈神经网络，其中第i层的神经元仅连接到第i + 1层的神经元，如图2.2所示。神经网络中具有后向连接的神经元称为循环神经网络，在对时间敏感的语音识别中非常有用。人工神经元在某种程度上模仿大脑内的生物神经元。然而，我们将把它们视为数学单元，因为与生物学的联系并不会使人们更容易理解它们的工作方式，除非有生物学背景。

从输入到输出 🔗

用于分类的神经网络接收一个输入向量X ∈ R^n，并输出一个向量Y ∈ R^c，代表可能类别的概率分布，如第2.3.1节所述。神经网络与其他分类器的不同之处在于它的工作方式。接下来我们将讨论这一点。

神经元的工作 🔗

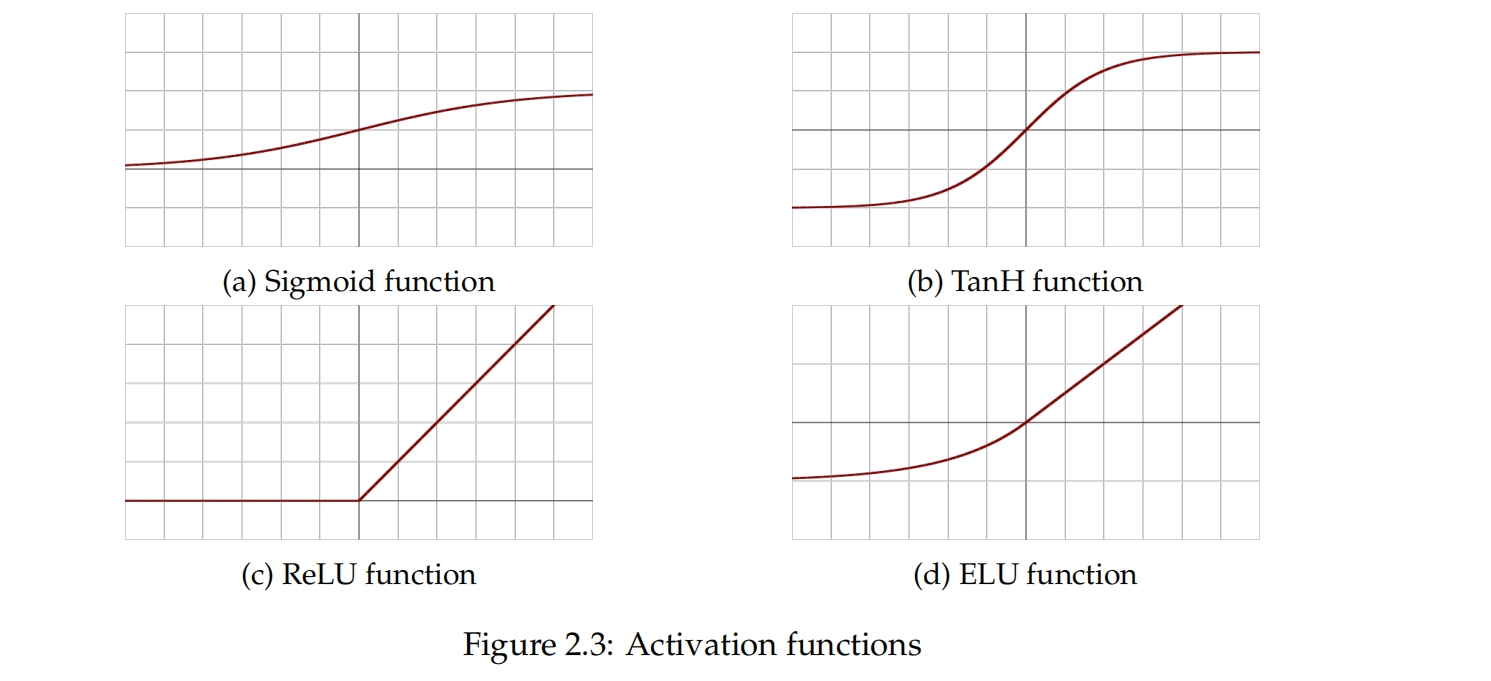
每个神经元对每个输入特征都有一个权重和一个偏差。它计算其输入的加权和，其中包括来自前一层的激活，如方程2.2所示，并应用激活函数。激活函数背后的思想是，神经元具有二进制输出，即它要么发射，要么不发射。每个神经元会检测来自前几层的输入中的模式，并在检测到模式时发射。它还在网络中引入非线性，这对于能够逼近非线性函数是必要的。

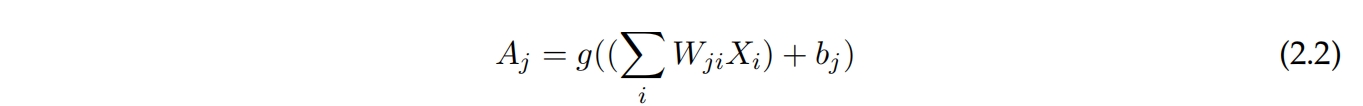
常见的激活函数是Sigmoid，如方程2.3所示。

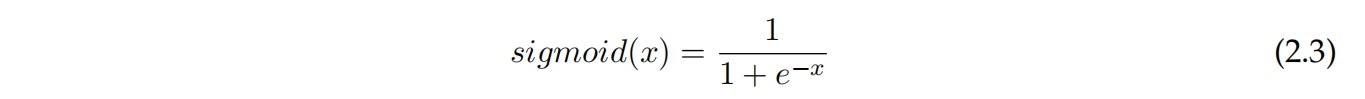
另一个常见的激活函数是TanH。

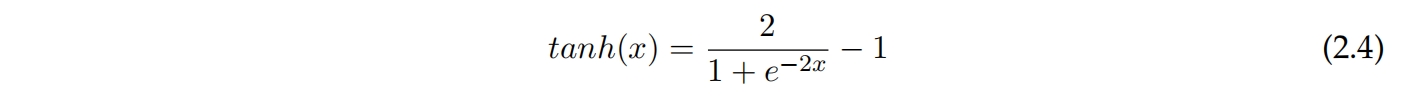
反向传播使用损失函数的梯度来更新神经网络的权重，因此如果梯度变得非常小，更新将变小，学习速度变慢。Sigmoid和tanh都存在梯度消失的问题，因为它们将输入映射到一个小范围内。方程2.5中显示的修正线性单元是另一个激活函数，它在处理梯度消失方面问题较少，因为它仅将负值截断为零。它训练速度是几倍快于Sigmoid和TanH，因为它不会饱和，意味着输出没有上限，可以变得任意大。它目前是深度学习中最流行的激活函数。

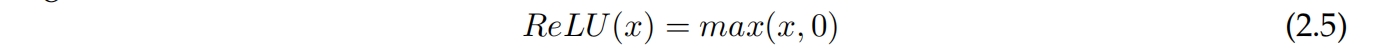
当输入被截断为零时，修正线性单元存在问题，因为这会使梯度变为零，无法进行学习。方程2.6中显示的指数线性单元(ELU)被引入来解决这个问题，允许负值存在。然而，与ReLU相比，ELU计算成本更高。

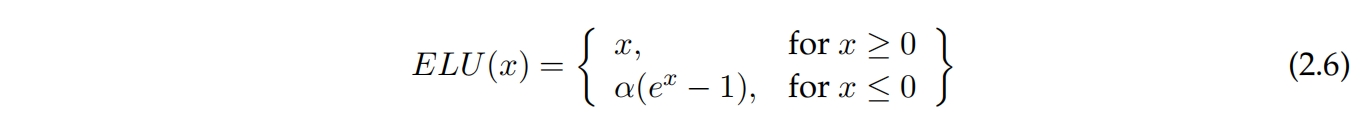
成本函数 🔗

为了改进神经网络，必须有一个客观的衡量标准来评估网络的表现好坏。这通过成本函数来实现。如果网络的输出接近期望输出，则成本较低，否则成本较高。一个常用的成本函数是均方误差，如方程2.7所示。

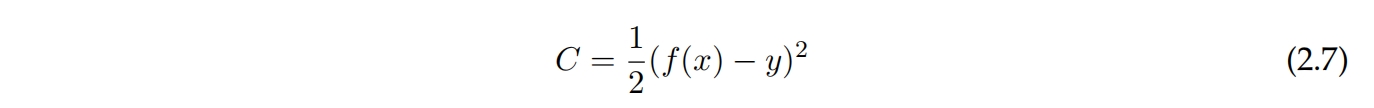
另一个常用的成本函数是交叉熵，它具有显著的实际优势，因为在权重随机初始化时可以找到更好的局部最优解[10, 11]。使用交叉熵成本函数而不是均方误差，结合softmax激活函数会导致更准确的结果[12]。

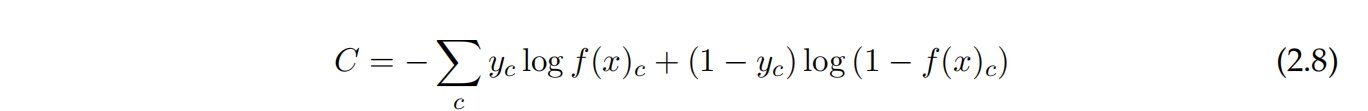
网络通过计算成本函数并更新其权重来学习，以最小化成本函数。因此，学习过程本质上是一个优化问题。成本函数是权重的函数。为了最小化它，使用梯度下降。梯度下降计算成本函数相对于权重的梯度。然后，它沿着相反的方向更新权重，使成本变小，如2.9所示。权重之间的差异大小由学习率决定。在实践中，对大量数据使用梯度下降不可行，因此改用随机梯度下降，仅使用训练数据的一个小子集来计算成本函数的估计值，这样可以加快训练时间 [13]。

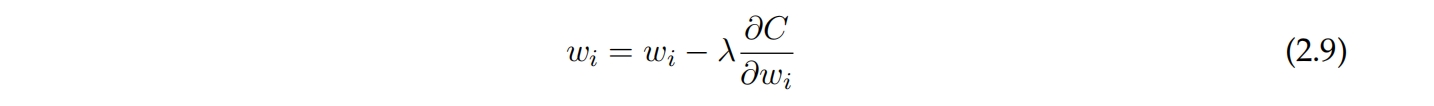
当神经网络进行训练时，它学习到应具有的权重。影响训练的参数，如网络架构，但在训练过程中不会学习的参数被称为超参数。神经网络有很多超参数。

• 学习率
• 隐藏层的数量
• 隐藏节点的数量
• 激活函数的选择
• 错误测量的选择
• 学习率衰减
• 正则化
• 初始权重

这些可以通过手动测试不同组合来决定。选择它们的更严谨的方法是使用网格搜索或随机搜索。在网格搜索中，为每个参数选择一个有限的值集合，然后尝试所有组合。产生最高准确性的组合被选为最佳参数组合。随机搜索是随机选择参数，已经显示比网格搜索更有效 [14]。基因算法通过结合先前成功的组合来培育新的组合，也可以被应用。一种基于强化学习的新颖方法，利用验证集上的验证准确性作为反馈生成架构，已被证明能够生成与CIFAR-10数据集上最佳人工设计的架构媲美的架构 [15]。

2.3.3 卷积神经网络 🔗

卷积神经网络（CNN）已经显著改善了物体识别，并且是目前此任务的最新技术 [16]。在CNN中，每个神经元连接在重叠的瓦片中，使网络在二维空间中具有局部性。这对可以被视为图像或网格的输入数据效果很好 [16]。 输入 将输入数据视为三维向量，而不是一维向量。一个尺寸为9×9的rgb图像将具有尺寸为9×9×3，因为它有3个颜色通道。 块大小 块大小决定一个神经元覆盖的面积有多大。3×3的块是最常见的大小，意味着第i+1层中的每个神经元都连接到第i层中一个3×3的神经元瓦片。 步幅 步幅确定输入之间每个到滤波器的距离。 滤波器 滤波器的数量决定每一层中可以检测到多少特征，因为滤波器共享权重。 池化 通过总结其输入来减小输入的维度。例如，一个2×2的最大池化将会接收一个2×2的输入，输出一个1×1，输出值为输入中的最高值，并跨数据进行步进。

2.4 Candy Crush 🔗

Candy Crush是一款在2012年发布在Facebook上的流行的三消游戏，后来在多个平台上推出。由于在开发超过2000个关卡过程中不断添加新功能，该游戏变得非常复杂。因此，我们不会提供游戏的完整描述，而是将读者引向在线可用的Candy Crush维基百科。我们将描述对论文有趣的基础知识。

2.4.1 基本游戏玩法 🔗

基本的游戏玩法包括在一个9x9的游戏板上水平或垂直交换相邻的瓦片，使得三个或三个以上的相同颜色糖果形成水平或垂直排列。这就是为什么它被称为三消游戏。如果忽略方向，有144种独特的交换组合，其中72种垂直和72种水平。

匹配的糖果将从游戏板上移除，如果匹配了三个以上的糖果，将会生成特殊糖果，如图2.5所示。特殊糖果比普通糖果更强大，因为它们在匹配时不仅会移除自身，还会移除其他糖果。制作特殊糖果因此是游戏策略中的重要部分。还有多种类型的阻碍物，如结霜，可能存在于一个瓦片上，使得在清除结霜之前，无法与下面的糖果匹配。

解决游戏是NP难题。状态空间在不同关卡之间不同，但是很大，实验显示第13关的状态空间约为10182。

2.4.2 游戏模式 🔗

有五种不同类型的关卡，具有不同的目标。

• 限时关卡：在时间耗尽之前达到特定分数
• 分数关卡：在固定次数的移动内达到特定分数
• 订单关卡：在固定次数的移动内清除所有订单，一个订单可能是清除90个红色糖果
• 组合关卡：完成其他目标的组合
• 配料关卡：在固定次数的移动内清除所有配料
• 凝胶关卡：在固定次数的移动内清除所有凝胶 具有不同策略要求的多种游戏模式使得游戏对AI更具挑战性。

第3章 🔗

方法 🔗

在本章中，我们详细描述了我们的方法。它分为两部分，即在简化版本的糖果上进行的实验和在糖果上进行的实验。

3.1 简化版糖果 🔗

当论文开始时，我们还没有来自糖果的训练数据，并且我们希望在简化问题上探索深度学习，以了解它对我们问题空间的强大性和适用性。因此，我们决定：

1. 构建一个简化版的糖果
2. 创建一个确定性贪婪机器人
3. 从贪婪机器人玩糖果中生成数据集
4. 训练一个深度神经网络（DNN）
5. 评估分类性能 由于我们没有任何关于简化版糖果的人类难度数据，因此我们在这个实验中不尝试预测难度。我们只探讨分类任务。

3.1.1 简化版糖果 🔗

简化版糖果是用C++实现的，可以带有或不带有GUI进行游玩。如图3.1所示。与真实游戏的9×9相比，它有一个略小的8×8游戏板。它有5种不同的糖果颜色而不是6种。它没有特殊糖果或阻碍物。它没有特定目标。游戏在60秒后自动停止，得分与清除的糖果数量成比例增加。新的糖果会从均匀分布中随机生成。

3.1.2 确定性贪婪机器人 🔗

我们创建了一个确定性贪婪机器人，它总是选择能清除最多糖果的移动。它总是更喜欢进行五连消而不是四连消，四连消而不是三连消。如果有多个移动能够清除相同数量的糖果，它更倾向于水平交换而不是垂直交换，并且更喜欢西北位置而不是东南位置。这使得机器人是确定性的，可以从任何游戏板上计算出它将选择的移动。这很重要，因为数据变得100%可预测，这意味着机器学习者可以获得100%的验证准确率。当从非确定性策略学习时，这是不可能的，您无法知道理论上的最大验证准确率是多少。

3.1.3 生成数据集 🔗

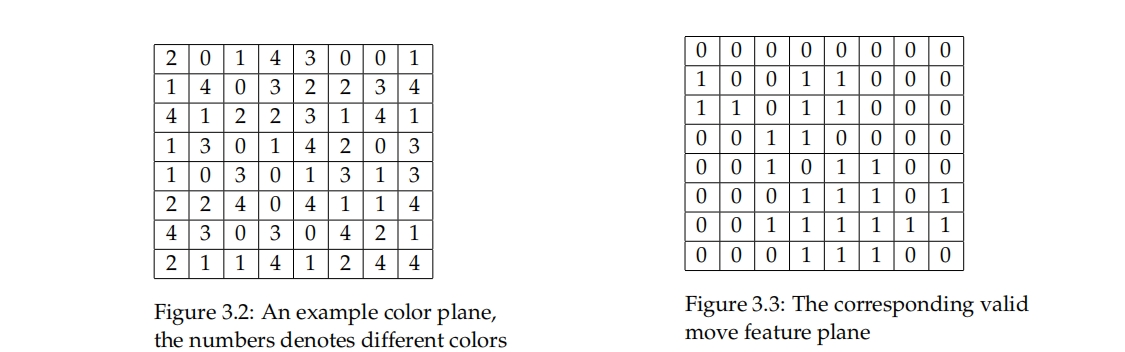
我们从确定性贪婪机器人玩简化版糖果中生成了一个数据集。数据集仅有两个特征平面，一个用于颜色，一个用于有效移动。每种颜色被编码为 0 ≤ c ≤ 4。有效移动特征平面是二进制的，对游戏板上的每个位置进行编码，表示该位置是否可以成为有效移动的一部分，意味着该单元格中的糖果可以交换并成为三连消的一部分。 由于游戏板有 board_size 行，每行有 board_size - 1 个水平交换（如果忽略交换的方向），所以一共有 board_size * (board_size - 1) 个水平交换。由于水平交换和垂直交换一样多，总交换次数为 2 * board_size * (board_size - 1)。对于这个特定的数据集，board_size = 8，因此有 2 * 8 * 7 = 112 种不同的交换。因此，一个移动被编码为一个数字，范围在 0 ≤ n ≤ 111，如图3.4所示。 数据集以CSV文件的形式存储。每一行对应一个数据点。前 2 * 8 * 8 = 128 个数字是特征，包含每个游戏板位置的两个特征平面，最后一个数字是移动。

3.1.4 神经网络架构 🔗

网络架构是通过手动实验决定的。我们本来希望在许多参数组合上执行网格搜索，但我们认为这样做太耗时且计算成本太高，在这项工作中并不切实可行。

我们选择使用卷积神经网络，因为我们的游戏板具有网格结构，并且在其他棋盘游戏（如围棋）上表现出色[1]。由于从MCTS机器人生成数据需要很长时间，所以在调整超参数时我们使用了比最终评估时更小的数据集。我们测试了不同数量的卷积层，发现超过三层不会提高验证准确性，反而会增加过拟合。池化操作通常用于减少输入维度，在图像识别中经常使用，例如图像大小为256x256。我们选择不使用池化操作，因为我们的9x9游戏板已经很小。

3.1.5 神经网络评估 🔗

数据集被分成训练集和验证集。训练集用于在训练过程中更新网络的权重。验证集用于评估。在训练过程中使用的性能衡量标准是验证准确性，如方程3.1所示。我们还计算了验证前2准确性和验证前3准确性，即在前2和前3个移动中正确移动被找到的频率。

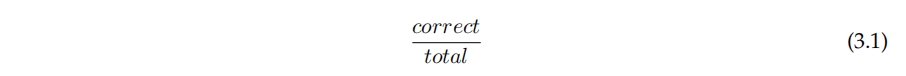
验证准确度并不是游戏策略的完美衡量标准，因为游戏状态中选择的动作是非确定性的，这意味着在某个游戏状态下，同一个玩家可能多次选择不同的动作。如果玩家在一个具有10个合法动作的状态下，以50%的概率选择其中一个动作，那么理论上的最大验证准确性将会是50%；但如果网络学习了正确的概率分布，它将完美地学习了游戏策略。理想情况是使用测量实际和预测概率分布之间距离的方法，而不是像方程3.2中所示的验证准确度，比如Kullback-Leibler散度。

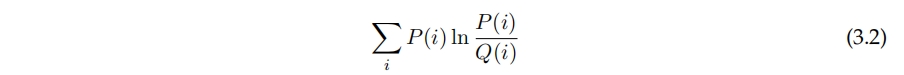
然而，由于状态空间非常大，很少有来自特定状态的多个训练样本，使得在特定状态下估计概率分布变得不可能。因此，出于务实原因选择了验证准确性。在没有其他基准的情况下，这被比较为随机选择每个游戏状态中移动的预期准确性，计算如方程3.3所示，其中Si是状态i中可用的移动数。

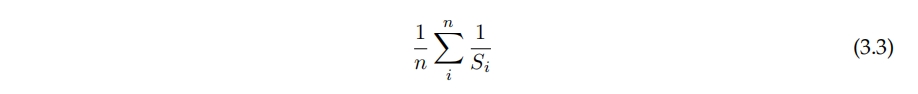
3.2 糖果 🔗

对糖果进行的实验包括以下步骤：

1. 从一个MCTS机器人玩糖果中生成数据集。
2. 训练一个DNN。
3. 使用DNN和MCTS玩不同的糖果关卡，并评估性能，以累积成功率和平均成功率作为衡量标准。
4. 评估表现，以累积成功率和平均成功率为指标进行测量。
5. 创建回归模型，从以尝试次数为单位的机器人难度测量人类难度来预测。

就像对简化版糖果一样，我们生成训练数据，然后训练神经网络，随后使用神经网络实际进行游戏，并根据成功率衡量机器人的表现，并创建一个模型来预测人类难度，其中机器人难度以每次成功尝试的次数来衡量。

3.2.1 蒙特卡洛树搜索 🔗

使用的MCTS算法由King提供。它是基于C++编写的，建立在糖果源代码的基础之上。这个实现有一些新颖之处。与其只使用胜利或失败作为信号不同，我们使用基于部分目标的连续信号，比如清除的果冻数量和/或得分。我们将其视为一个黑盒子，可以在模拟游戏过程中配置为使用训练过的DNN，因此不需要更详细的描述，但在Erik Poromaas的硕士论文中有更多信息。

3.2.2 生成数据集 🔗

由于我们希望使用神经网络来预测玩家的难度，最合理的做法是使用玩家的游戏数据。然而，该数据并不可用，我们无法在论文中获取到。我们有一个可以很好地玩游戏的MCTS机器人。我们让这个MCTS机器人在每次移动时使用1000次模拟游戏来玩一个多样化的关卡集，这些关卡从第1000关到第2000关，并在游戏过程中记录所有的（状态，动作）对，以CSV格式直接用于训练神经网络。我们收集了接近200万个数据点。其中50,000个数据点用于验证，其余用于训练。

数据表示 特征平面包括：

1. 可用的水平移动次数
2. 可用的垂直移动次数
3. 缺失的瓷砖
4. 糖果颜色 - 随机
5. 糖果颜色 - 无
6. 糖果 - 蓝色
7. 糖果 - 绿色
8. 糖果 - 橙色
9. 糖果 - 紫色
10. 糖果 - 红色
11. 糖果 - 黄色
12. 糖果颜色数
13. 果冻
14. 障碍物
15. 锁定物
16. 普通类型的板块物品
17. 行类型的板块物品
18. 列类型的板块物品
19. 包装类型的板块物品
20. 热门类型的板块物品
21. 炸弹类型的板块物品
22. 瑞典鱼类型的板块物品
23. 食材类型的板块物品 - 樱桃
24. 食材类型的板块物品 - 榛果
25. 时间补充类型的板块物品
26. 辣椒糖果类型的板块物品
27. 甘草糖果类型的板块物品
28. 椰子轮类型的板块物品
29. 王牌类型的板块物品
30. 神秘糖果类型的板块物品
31. 变色糖果类型的板块物品
32. 青蛙类型的板块物品
33. 榛子类型的板块物品
34. 不明飞行物类型的板块物品 - UFO
35. 板块物品类型数
36. 剩余移动次数

颜色被编码为单独的二进制特征平面，与简化的数据集不同，在简化的数据集中只有一个颜色特征平面，不同的颜色使用不同的数字。这样做更有意义，因为颜色只有分类意义。有效移动的特征平面被划分为水平移动和垂直移动两部分。这并不会造成任何差异，因为神经网络能够学习两种表示。移动的编码与第一个实验中的相同，只是更大的游戏板面使得0 ≤ n ≤ 143，而不是如图3.5中的0 ≤ n ≤ 111。

缺点 虽然在简化版的糖果游戏中移动的方向并不重要，但在糖果游戏中却很重要。当匹配两种特殊糖果时，对游戏板的影响会因方向的不同而不同。为了捕捉到这种情况，我们需要区分288种移动，而不是144种。这可能使得学习到需要特定的特殊糖果和方向组合才能过关的高级策略变得不可能。然而，我们注意到我们有50%的概率能够在最佳的方向进行交换，并且两个相邻的条纹糖果并不是一个常见的情况，所以我们决定丢弃方向，因为如果类别增加一倍，会使得训练DNN变得更加困难。 数据集还有其他一些缺点。最大的一个是没有关于关卡目标的特征平面。如果目标是清理果冻，数据中并未包含需要清理的果冻数量，如果目标是清理材料，那么也没有包含剩余需要清理的材料数量的特征平面。这可能会使网络在剩余移动次数较少的情况下，难以学会优先考虑目标，而不是创建花哨的特殊糖果。

3.2.3 DNN架构 🔗

我们使用与简单糖果游戏相同的DNN。

3.2.4 使用DNN 🔗

因为我们认为使用不成熟的TensorFlow C++ API将其嵌入到MCTS C++源代码中过于繁琐，所以我们通过用Python编写的HTTP服务器使用DNN。让HTTP服务器在与机器人相同的物理机器上运行，使得网络开销微乎其微。 我们试验让DNN独自玩游戏以及在MCTS播放过程中玩游戏。根据DNN选择最有可能的移动。

3.2.5 神经网络评估 🔗

对于简单的糖果游戏，训练的评估方式相同。我们总共使用了4个机器人进行比较。机器人也与人类玩家进行比较。我们比较了机器人的累积成功率，以衡量他们的表现。我们还拟合了模型，以预测从机器人每个成功的尝试次数中预测人类每个成功的尝试次数，以衡量它们的预测力。MCTS每个级别执行100次尝试，DNN每个级别执行100和1000次尝试，因为它的速度更快。

随机机器人 随机机器人从均匀分布中随机选择动作。这是默认的基线。

DNN机器人 DNN机器人根据深度神经网络选择最可能的动作。它不进行任何搜索。

MCTS + 随机机器人 MCTS + 随机机器人使用随机回放的MCTS。它作为MCTS + DNN机器人的基线。

MCTS + DNN机器人 MCTS + DNN机器人在回放过程中使用MCTS，其中根据DNN选择最可能的动作。

3.2.6 预测模型 🔗

我们让机器人玩361个级别，以计算机器人试错次数的难度。我们让每个机器人对每个级别尝试100次，除了DNN，我们允许其尝试1000次，因为它的速度更快。这些级别的玩家数据是可用的，所以我们也可以计算人类每次成功的尝试次数。机器人的难度并不等同于人类的难度，但它们是相关的。我们拟合了一个回归模型来预测机器人尝试成功次数到人类尝试成功次数。我们使用平均绝对误差作为预测精度的度量，这直观地表示预测的平均错误程度。

我们将级别分为三组，绿色，黄色和红色，根据他们对每个级别的难度，因为我们看到人类每次成功的尝试次数和机器人每次成功的尝试次数的关系，对于更简单的级别和更困难的级别是不同的。我们为每个机器人的每个组拟合一个单独的预测模型。绿色级别的尝试成功率低于或等于预选的割值。黄色级别的成功尝试次数高于割值。红色级别有零成功，所以尝试次数是未定义的。我们使用人类每次成功尝试的平均值作为红色级别的预测值。

3.3 软件 🔗

我们使用深度学习库TensorFlow来实现DNN。Google创造了TensorFlow来替代在Google内部广泛使用的DistBelief [18]。TensorFlow是用C++编写的，API在Python中可用。它不像其他如Torch和Theano[19]等可用的深度学习库那么快，但有很多有用的工具。TensorBoard是一个可视化训练的Web界面。在创建TensorFlow图时，可以添加用于记录如验证精度、交叉熵和学习率等测量值的节点。TensorBoard可以在训练中动态创建的图中显示登记的测量值，如图3.7所示。

3.4 硬件 🔗

我们使用了来自亚马逊网络服务的一个g2.8xlarge GPU服务器用于训练神经网络。它具有：

• 4个GPU
• 32个vCPU
• 60 GiB内存
• 2x120 SSD存储

游戏在具有未知规格的虚拟机上运行。

第4章 🔗

结果 🔗

4.1 训练神经网络 🔗

这部分展示了在训练过程中DNN的表现。验证精度显示了DNN在未见过的数据上预期的表现。我们还包括了正确的动作在前2和前3中出现的频率。训练的最终结果和使用的数据集的详细信息显示在表4.1中。训练期间的验证精度的图示显示在图4.1和图4.2中。

在简化的数据集上的验证精度很高，如表4.1所示，达到了92.2%。如果给出更多的数据，更多的训练时间和更大的模型，它可能会变得更好。可能接近100%。

在MCTS数据上的验证精度要低得多，只有28.3%。这并不奇怪，因为它是由一个非确定性的算法生成的。28.3%依然比随机猜测的16.3%要高很多。考虑到我们不知道MCTS数据的可预测性如何，很难知道我们的网络在学习它方面的表现如何。可能是30%是理论上的最高验证精度，如果是这样，那么28.3%就是很好的结果，或者可能会更高，如果是这样，那么28.3%可能就不太好了。为了了解DNN在学习像MCTS那样玩游戏的情况如何，我们需要用DNN玩游戏，并比较它和MCTS的表现。我们将在下一节中做这个。

训练精度在图表中跳动较大。这是因为它是在128个随机选择的数据点上计算的。对于两个数据集，训练精度似乎接近验证精度。这意味着神经网络没有过拟合，说明还有增加模型大小的空间。我们本来会做这个，但是时间不够。在论文工作期间，我们不断地收集更多的数据，直到最后一个数据集足够大，也就没有过拟合。

看着验证，验证前-2和验证前-3的精度，我们注意到，在MCTS数据上训练的DNN从28.3%提高到44.4%，再提高到57.3%。这意味着即使它没有选择正确的动作，正确的动作往往也在前3之内。考虑到在糖果游戏中有许多情况，多种动作看起来同样好，如果很难在它们之间区分也就不足为奇了。

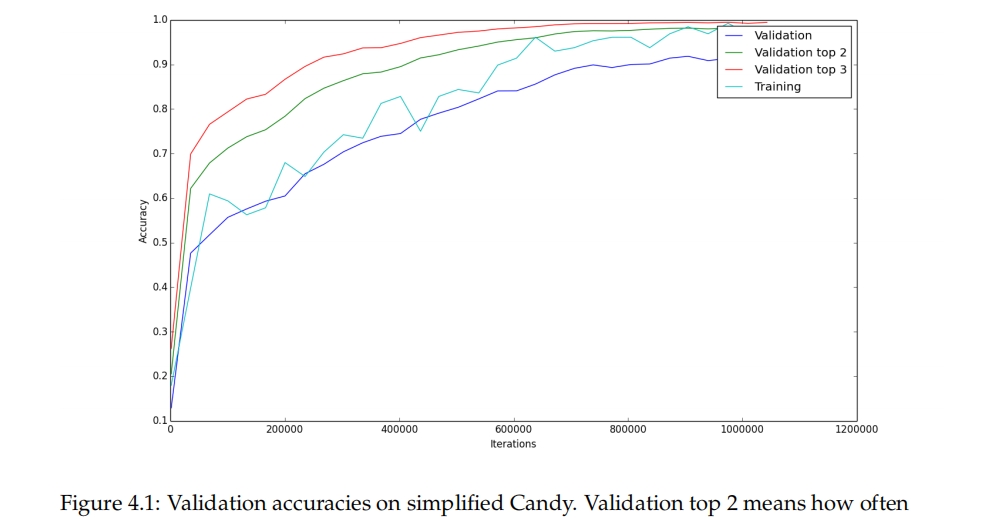
图4.1：简化糖果游戏的验证精度。验证前2意味着正确的动作在预测的前2个中的频率，验证前3意味着正确的动作在预测的前3个中的频率。训练精度是在128个数据点的小批量上计算的。

表4.1：简化糖果游戏和糖果游戏的神经网络训练结果。随机精度是从每个游戏状态的可用移动中随机选择时所期望的验证精度。训练精度是在训练数据的一个小型批次上计算的。验证前-2精度和验证前-3精度意味着正确的动作在预测动作的前-2和前-3中的频率。

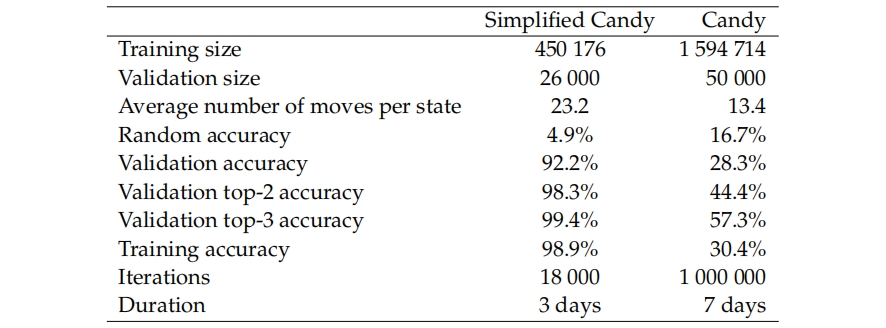
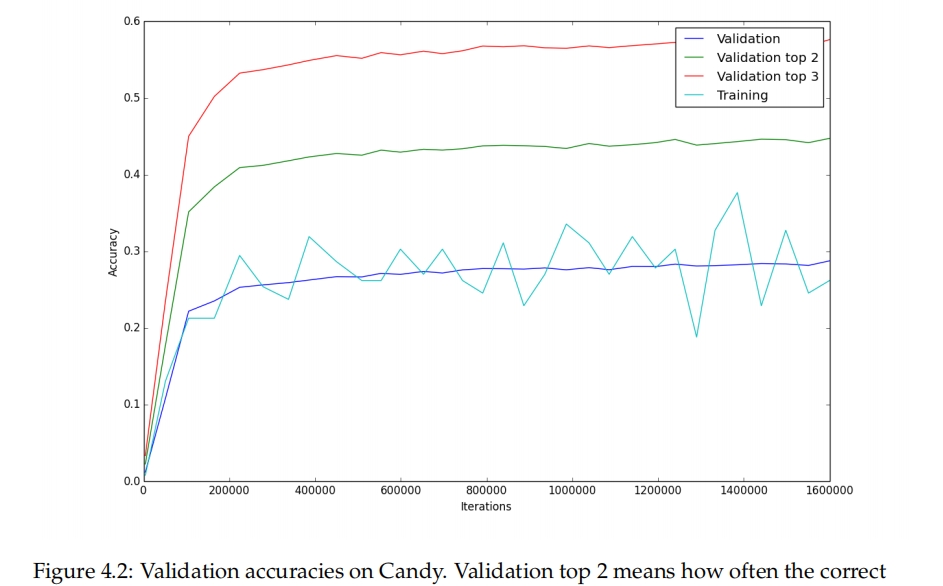
图4.2：糖果游戏的验证精度。验证前2意味着正确的动作在预测的前2个中的频率，验证前3意味着正确的动作在预测的前3个中的频率。训练精度是在128个数据点的小批量上计算的。

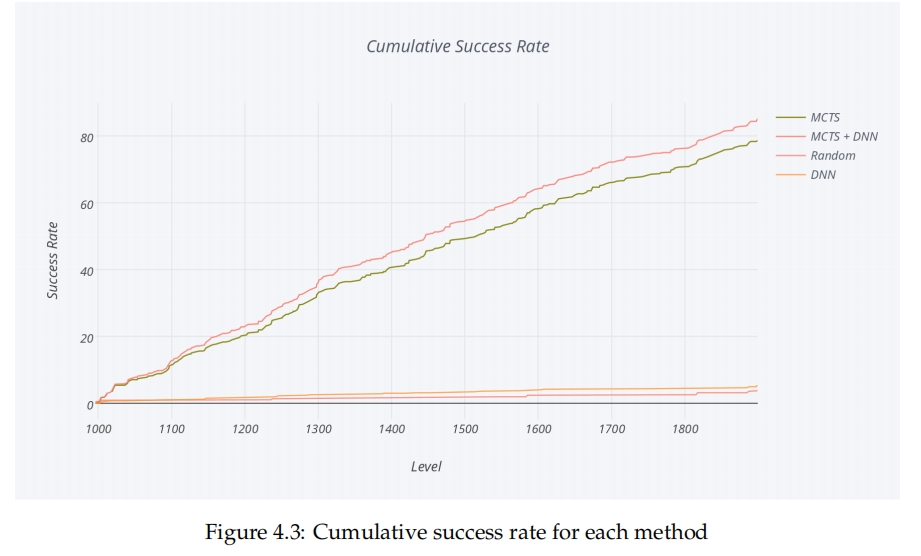
4.2 机器人性能 🔗

我们使用图4.3中显示的所有等级的累积成功率来比较机器人的强度，数值越高越好。 在不进行任何搜索的情况下，深度神经网络(DNN)的表现优于随机选择，如图4.3所示，在进行模拟过程中使用DNN可以提高蒙特卡洛树搜索(MCTS)的性能。这证明了DNN已经从数据中学到了游戏的有用知识，但肯定还有很多没有学到。值得注意的是，纯粹的DNN的表现与纯粹的MCTS相比差很多，而其他人已经成功地使DNN在围棋中的表现与MCTS一样强。围棋的结果是使用专家的动作实现的，而我们使用的数据是来自于比专家玩家更弱的MCTS机器人。训练数据的问题之一是它没有包含游戏的目标。出于这个原因，如果不进行任何搜索，表现好就将变得困难。使用搜索与不使用搜索之间的改进要大于使用DNN与不使用DNN之间的改进。

4.3 难度预测 🔗

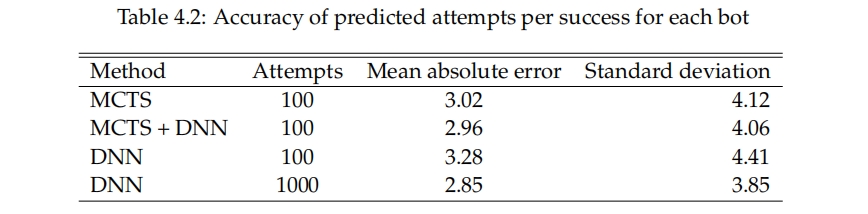
表4.2显示了每个机器人在361个级别的平均绝对误差。这显示了模型从机器人的难度中预测人类难度的能力有多好。 最令人惊讶的结果是，尽管深度神经网络(DNN)比蒙特卡洛树搜索(MCTS)弱很多，但是当它被允许在每个级别尝试1000次而不是100次时，它在预测人类难度方面却和MCTS差不多，或者更好，可以在表4.2中看到。当DNN在每个级别只做100次尝试时，它是最差的预测器。由于DNN比MCTS快得多，所以它可以在比MCTS做100次尝试的时间更短的时间内做1000次尝试。

第5章 讨论与结论 🔗

5.1 实践的有效性 🔗

深度神经网络（DNN）如果被允许进行1000次尝试而不是100次，它能做出与蒙特卡洛树搜索（MCTS）相似的难度预测，这是一个在实践中有实用性的结果。这意味着在几分钟内，而不是几个小时，就可以得到与人类难度相似的估计。这可以改变关卡设计师的工作流程，给他们提供更快的反馈循环，使他们在发布前有可能做出更多的调整。

5.2 方法在Candy Crush以外的适用性 🔗

我们用来预测Candy Crush游戏难度的方法也应该适用于其他游戏。游戏需要有一个有限的动作空间，这样就可以将其解释为一个分类问题，而且由于我们只是看当前的游戏状态来选择一个动作，所以动作的选择必须只依赖于当前的游戏状态，而不是前一状态。在King公司，我们在两个其他的游戏中也应用了相同的方法，但是那些游戏与Candy Crush非常相似。这种方法对频繁发布新关卡的游戏最有用。

5.3 深度神经网络和蒙特卡洛树搜索对比 🔗

DNN方法的主要优势是速度，可以在极短的时间内做出相似的难度预测。DNN的另一个好处是，它可以在人类的游戏数据上进行训练，使其能像人类一样游戏，可能导致更精确的预测。DNN的主要劣势是，它需要游戏数据和重新训练。对于每一个新的游戏，都必须创建一个游戏状态表示并收集数据。每当游戏添加新的游戏元素时，DNN就必须进行重新训练，并收集新的数据以保持精度。MCTS不需要任何关于游戏版面的知识，因此相同的算法可以应用于新的游戏，无需修改。

5.4 人工智能的伦理学 🔗

人工智能（AI）存在两个主要关注点。一是超级智能的威胁，二是自动化的经济影响。 超级智能 人工智能可根据其强大的程度分为三种类别。目前所有的AI都处于人工狭义智能（ANI）的类别，也就是说它是特定任务。深蓝（DeepBlue)比任何人都擅长下棋，但下棋是它能做的全部。第二个类别是人工普遍智能（AGI），包括大约与人类一样能力的AI，也就是说它能做人类可以做的普通事情。第三类是人工超智能（ASI），包括超过人类的AI。一旦AGI被发明出来，它可能能够递归地改进其软件以使其更有能力，最终达到ASI [20]。如果ASI变得恶性，它可能会将人类消灭。在这篇论文中，我们探讨了ANI的另一种应用，它在当前状态下并不对人类的生存构成威胁。

经济影响 能以更低的价格取代人类劳动的AI会导致失业，至少在冗余的工人找到替代工作的时候是暂时的 [21]。一些工人可能会发现很难转换到新的职业，因为他们可能没有或者不能获得需要的技能。这篇论文可能会使游戏的人工测试者变得多余和失业。

环境影响 所述方法需要在云服务器上使用计算能力和存储，但让一个计算机程序在几秒钟内玩一个级别应该比让一个人在几分钟内玩它有更小的环境影响，因此我们认为，用自动化解决方案成功地替换人工玩家对环境是有好处的。

5.5 未来的工作 🔗

改进架构 由于我们受到时间的严重限制，我们并没有对可能的神经网络的空间进行过多的探索。有几乎无尽的事物可以试验。如果有时间的话，用更多的数据训练更深层的DNN可能会显示出更好的结果。我们并没有在我们的架构中出现过拟合，所以训练一个更深层次的DNN将是下一步要尝试的事情。

改进数据 我们使用的数据排除了重要信息，如关卡的目标。它也没有包含移动的方向。使用更优质的数据可能会显示出更好的结果。

真实用户数据 我们最初打算在这篇论文中使用真实用户的数据。我们花了很多时间收集《糖果粉碎苏打传奇》的数据，这需要向代码库添加代码并发布。然而，由于回放游戏的问题超出了我们的控制范围，这一任务不得不中止。继续进行这个实验，对专家玩家进行训练，并观察这对性能有何影响，将是一个有趣的话题。

强化学习 在这篇论文中，我们只尝试让神经网络学习别人如何玩，本例中是一个MCTS Bot。被最小化的性能指标是神经网络能多好地预测别人如何玩。将目标改为尽量打好可能是个有趣的尝试。使用强化学习，可以在对数据集进行训练后修改DNN的权重，以便最大化其性能。玩一关，看看它的表现如何，更新权重，让它下次玩得更好。

学习的定性探索 我们只对性能进行了定量度量。神经网络学习了什么样的动作和策略？我们并不清楚，我们只知道它达到了一定的验证精度，而且它在游戏中有一定的成功率。探究它学习了哪些动作，没有学习哪些动作，可能会给出一些有趣的见解。

5.6 结论 🔗

我们研究了使用基于深度神经网络(DNN)的机器人玩《糖果粉碎传奇》游戏以预测游戏水平难度，并将其与基于蒙特卡洛树搜索(MCTS)的机器人进行了对比。我们在MCTS机器人生成的数据上训练了DNN。DNN机器人比MCTS机器人弱得多，但它可以用来在更短的时间内做出与MCTS机器人相当的人类难度预测。DNN也可以通过在决策过程中使用，而不是随机决策，来使MCTS机器人更强大，但由此做出的人类难度预测并没有更准确。最重要的三个结论是：

• MCTS比DNN强大得多
• 如果在游戏过程中使用DNN，可以使MCTS更强大
• DNN可以在大大缩短的时间内做出与人类难度相当的预测

参考文献 🔗

[1] David Silver, Aja Huang, Christopher J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, John Nham, Nal Kalchbrenner, Ilya Sutskever, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel 和 Demis Hassabis. 利用深度神经网络和树搜索掌握围棋。《自然》杂志, 529:484–503, 2016。网址http://www.nature.com/nature/journal/v529/n7587/full/nature16961.html。 [2] Erik Poromaa. 《粉碎糖果传奇》的胜利。硕士论文, 皇家工学院, 2016。 [3] Alex Krizhevsky, Ilya Sutskever, 和 Geoffrey E Hinton. 利用深度卷积神经网络进行Imagenet分类。在神经信息处理系统进展中, 页码1097–1105, 2012。 [4] Chris J. Maddison, Aja Huang, Ilya Sutskever, 和 David Silver. 利用深度卷积神经网络在围棋中进行着法评估。CoRR, abs/1412.6564, 2014。网址http://arxiv.org/abs/1412.6564。 [5] Barak Oshri 和 Nishith Khandwala. 使用卷积神经网络预测国际象棋中的着法。 [6] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, 和 Martin Riedmiller. 使用深度强化学习玩Atari游戏。arXiv预印本arXiv:1312.5602, 2013。 [7] Levente Kocsis 和 Csaba Szepesvári. 基于赌徒蒙特卡罗规划的带头臂策略。在机器学习欧洲会议上, 页码282–293。Springer, 2006。 [8] Yann LeCun, Yoshua Bengio, 和 Geoffrey Hinton. 深度学习。《自然》, 521(7553):436–444, 2015。 [9] Djork-Arné Clevert, Thomas Unterthiner, 和 Sepp Hochreiter. 通过指数线性单元（ELUs）快速准确地学习深度网络。CoRR, abs/1511.07289, 2015。网址http://arxiv.org/abs/1511.07289。 [10] Pavel Golik, Patrick Doetsch, 和 Hermann Ney. 交叉熵与平方误差训练：理论和实验比较。在Interspeech中, 页码1756–1760, 2013。 [11] Douglas M Kline 和 Victor L Berardi. 重新审视用于训练神经网络分类器的平方误差和交叉熵函数。神经计算与应用, 14(4):310–318, 2005。 [12] Rob A Dunne 和Norm A Campbell. 关于softmax激活和交叉熵惩罚函数配对以及softmax激活函数的推导。在第8届澳大利亚神经网络会议论文集中, 墨尔本, 181, 卷185, 1997。 [13] Michael A. Nielsen.《神经网络与深度学习》。Determination Press, 2015。 [14] James Bergstra 和Yoshua Bengio. 超参数优化的随机搜索。《机器学习研究杂志》, 13(Feb):281–305, 2012。 [15] Barret Zoph 和Quoc V. Le. 利用强化学习进行神经网络架构搜索。CoRR, abs/1611.01578, 2016。网址http://arxiv.org/abs/1611.01578。 [16] Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, 和 Andrew Rabinovich. 使用卷积进一步深入。在IEEE计算机视觉与模式识别大会论文集中, 页码1–9, 2015。 [17] Toby Walsh. 糖果传奇是NP难题。CoRR, abs/1403.1911, 2014。网址http://arxiv.org/abs/1403.1911。 [18] Martín Abadi, Paul Barham, Jianmin Chen, Zhifeng Chen, Andy Davis, Jeffrey Dean, Matthieu Devin, Sanjay Ghemawat, Geoffrey Irving, Michael Isard, 等. TensorFlow: 一个大规模机器学习系统。在第12届USENIX操作系统设计与实现研讨会（OSDI）论文集中。美国乔治亚州萨凡纳, 2016。 [19] Soheil Bahrampour, Naveen Ramakrishnan, Lukas Schott, 和Mohak Shah. 深度学习软件框架的比较研究。arXiv预印本arXiv:1511.06435, 2015。 [20] Nick Bostrom. 超级智能出现前需要多长时间？1998。 [21] Nils J Nilsson. 人工智能、就业和收入。《人工智能杂志》，5(2):5, 1984。

结论 🔗

搬砖愉快！