3D数学是一门和计算几何相关的学科,计算几何则是研究用数值方法解决几何问题的学科。
游戏数学 🔗
向量(Vector) 🔗
在物理、工程中又称矢量,指一个同时具有大小和方向,且满足平行四边形法则的几何对象。向量不关心绝对的开始位置,将向量平移到任何地方,向量始终一致。

Verctor Normalization 🔗
单位向量,长度为一个单位(即模为1)的向量,叫做单位向量。一般用来表示方向向量,不关心其长度。
Verctor Addition 🔗
向量加法,满足平行四边形法则和三角形法则。具体地讲两个向量A和B相加,得到另一个向量,这个向量可以表示为向量A和B的起点重合后,以它们邻边构成的平行四边形对角线,或者表示为向量A的起点执行向量B的终点的向量。
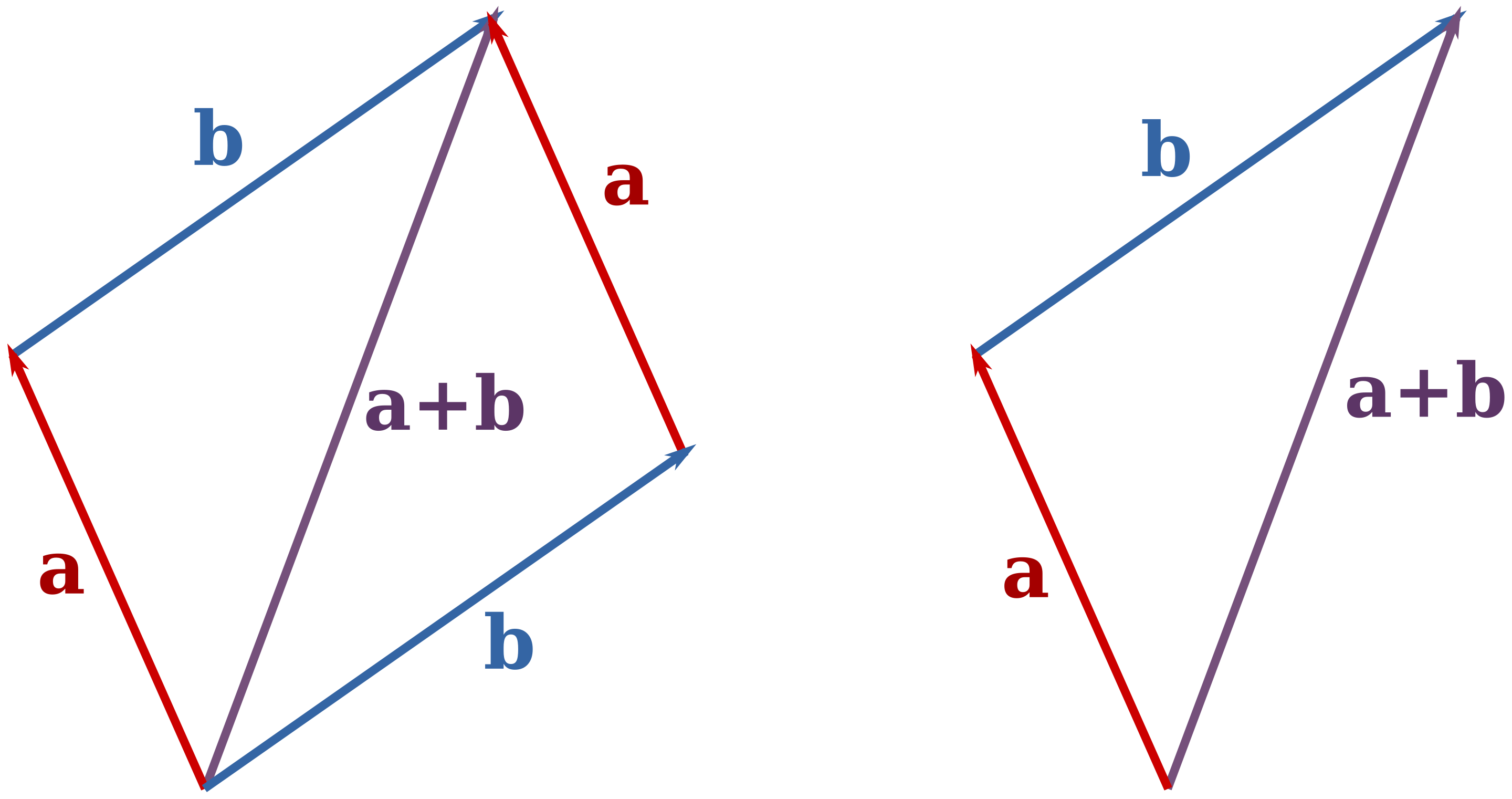
Vector Subtraction 🔗
向量减法,两个向量A和B相减,向量A加上一个向量B大小想等,方向相反的向量。
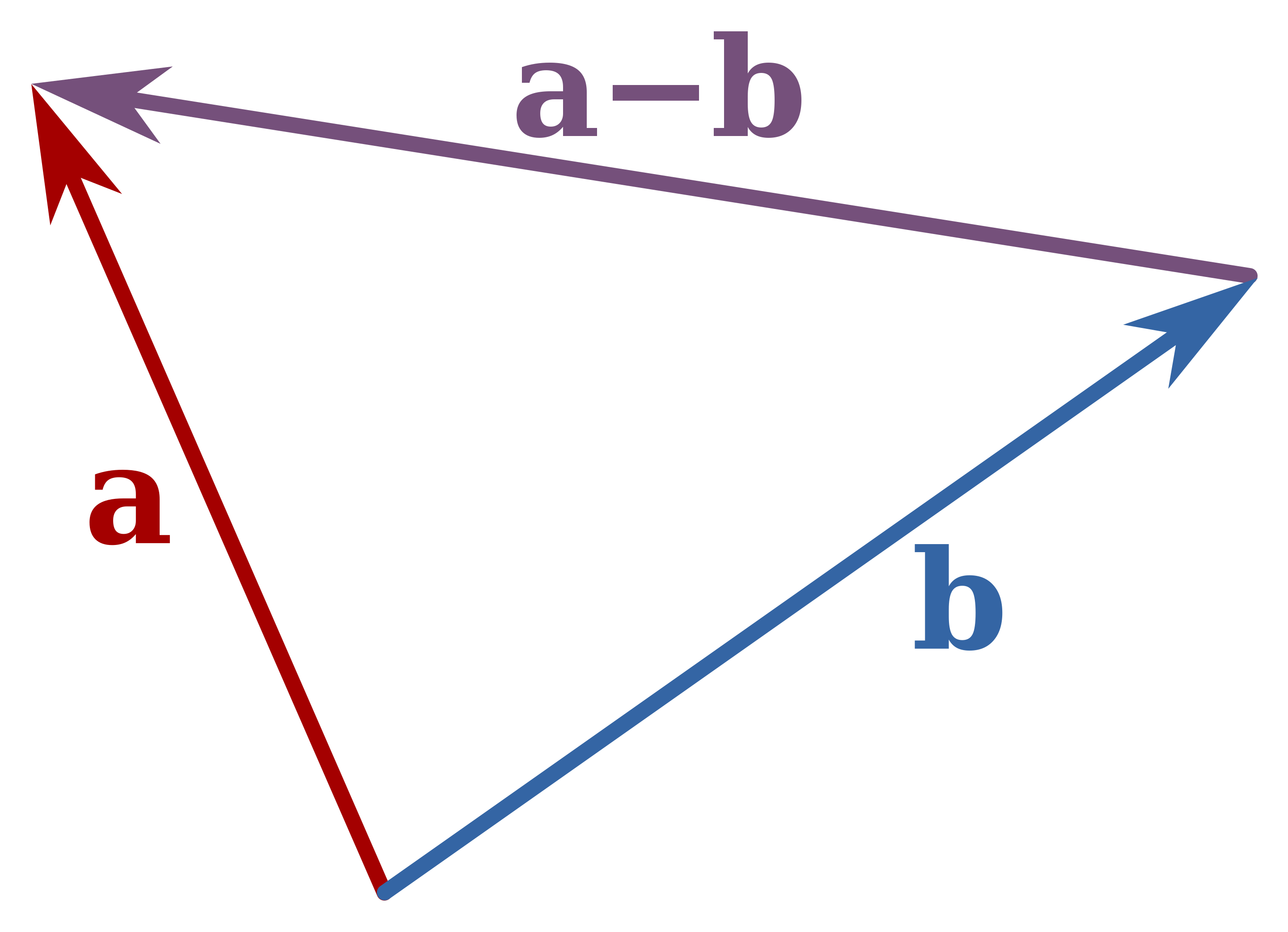
Dot Product 🔗
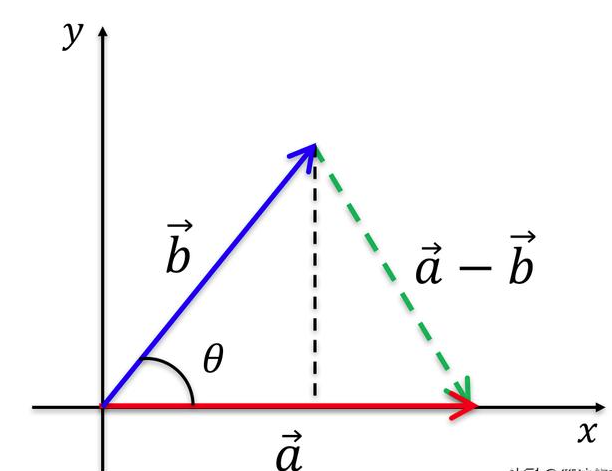
点乘的数学定义:

点乘的几何意义:

向量的点乘可以用来计算两个向量之间的夹角,进一步判断这两个向量是否正交(垂直)等方向关系。同时,还可以用来计算一个向量在另一个向量方向上的投影长度。
Cross Product 🔗
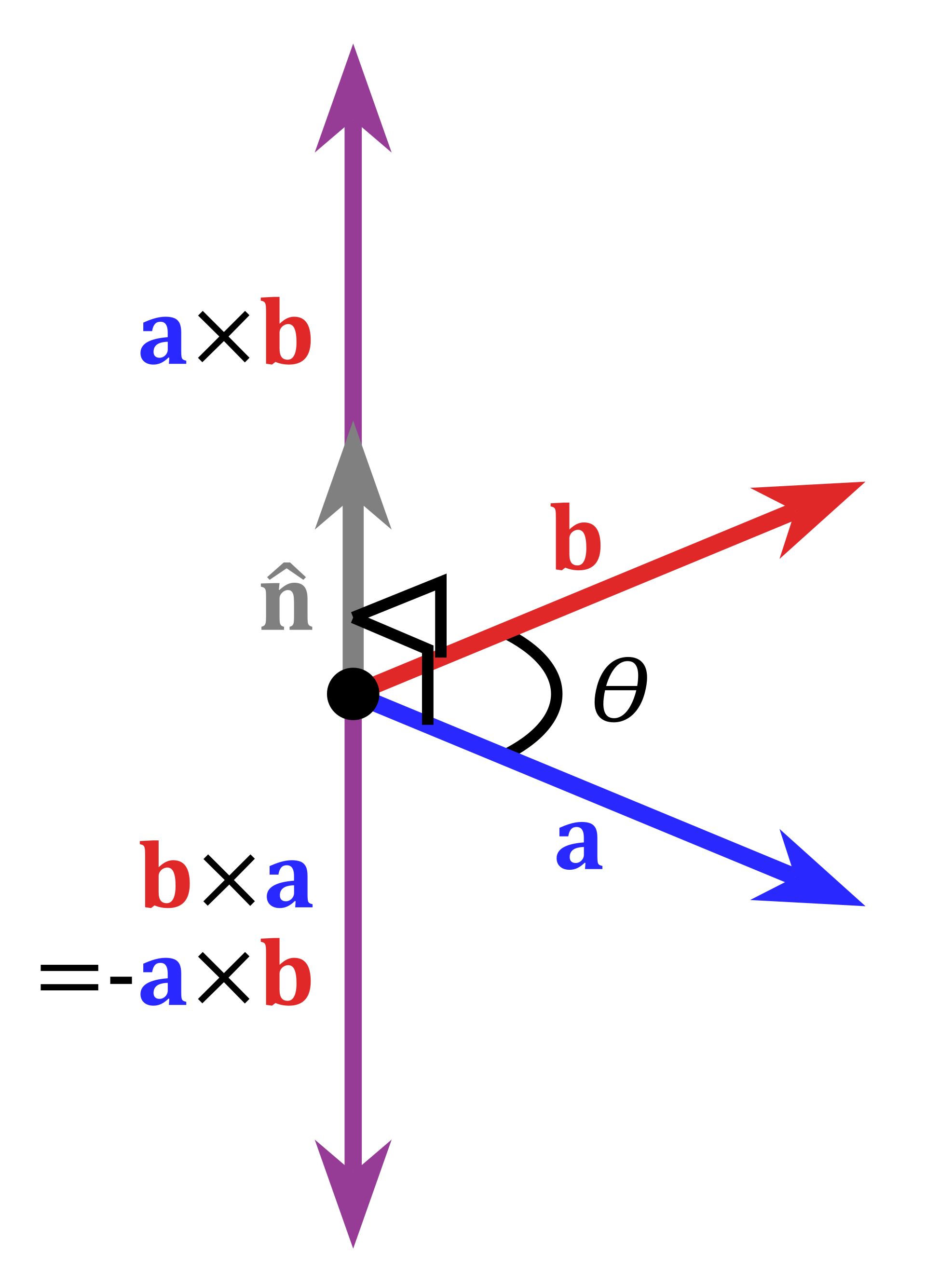
叉乘的数学定义:
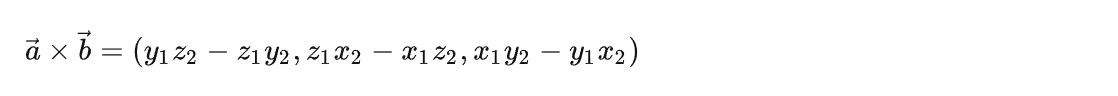
叉乘的几何定义:

运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。叉乘根据右手定则确定其方向。
叉乘的几何意义:
1、构建指教坐标系
2、构建向量a和向量b的平行四边
3、判断向量左右,判断向量的内外
矩阵(Matrix) 🔗
矩阵是一种描述线性变换的数学工具。
矩阵的基本运算

矩阵不符合交换律,符合结合律。
Matrix-Vector Multiplication 🔗
矩阵和向量相乘
将向量写成M * 1的列向量
确保矩阵能和M*1矩阵相乘
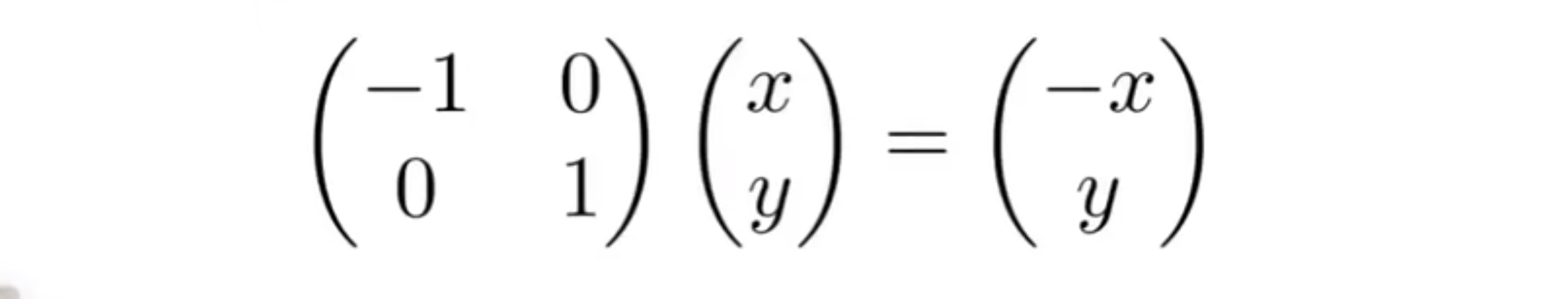
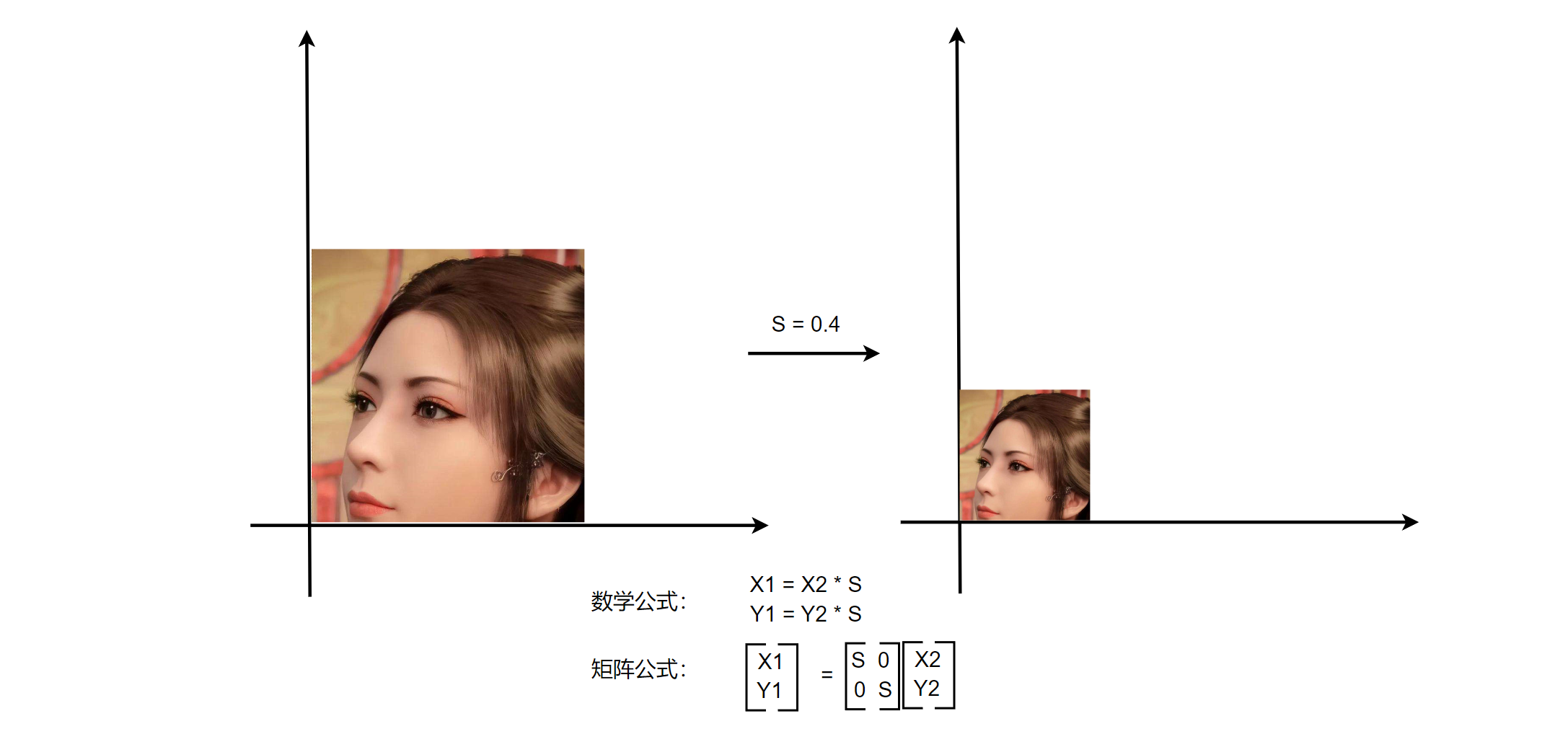
2D - Scale Matrix 🔗
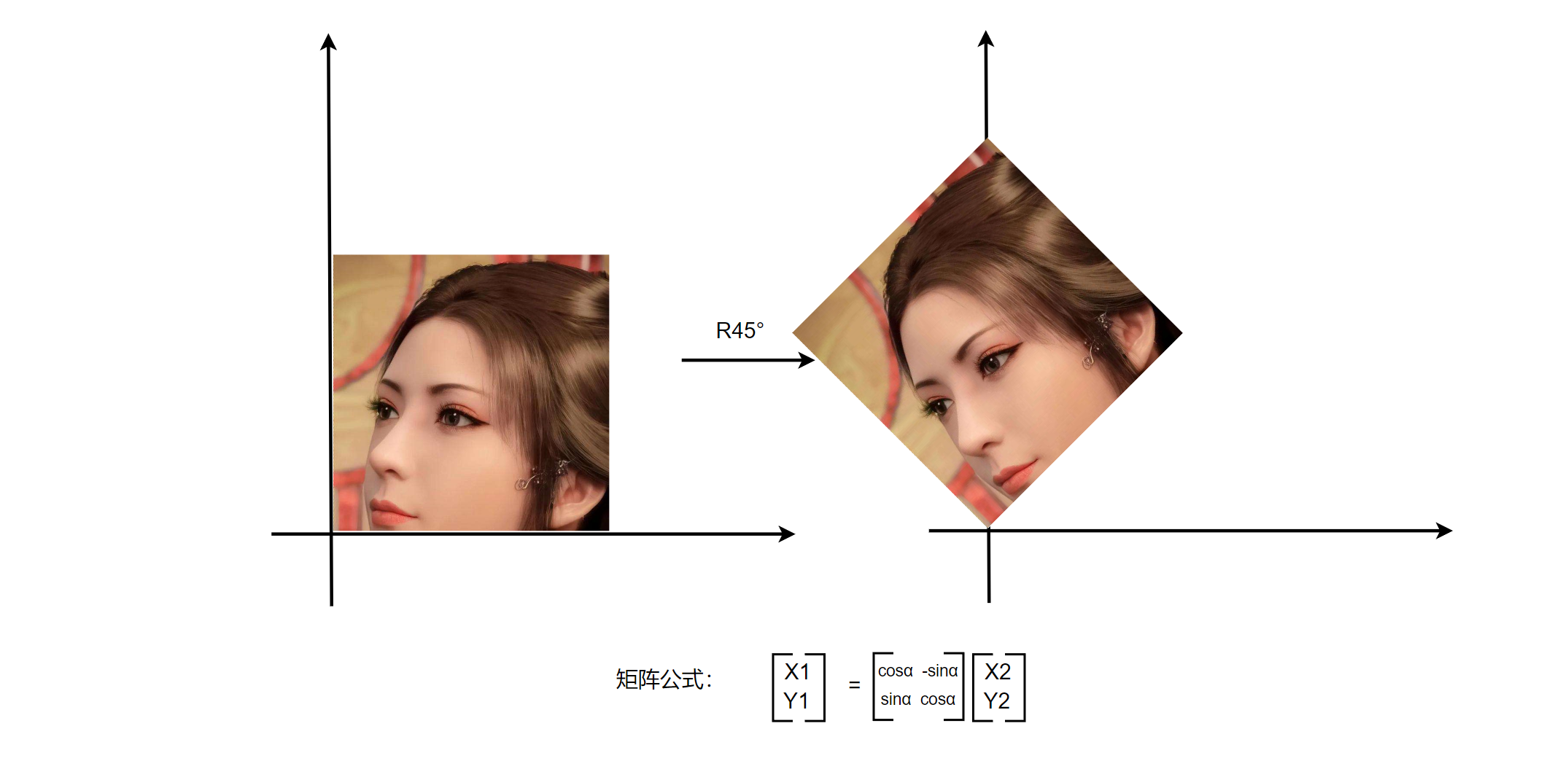
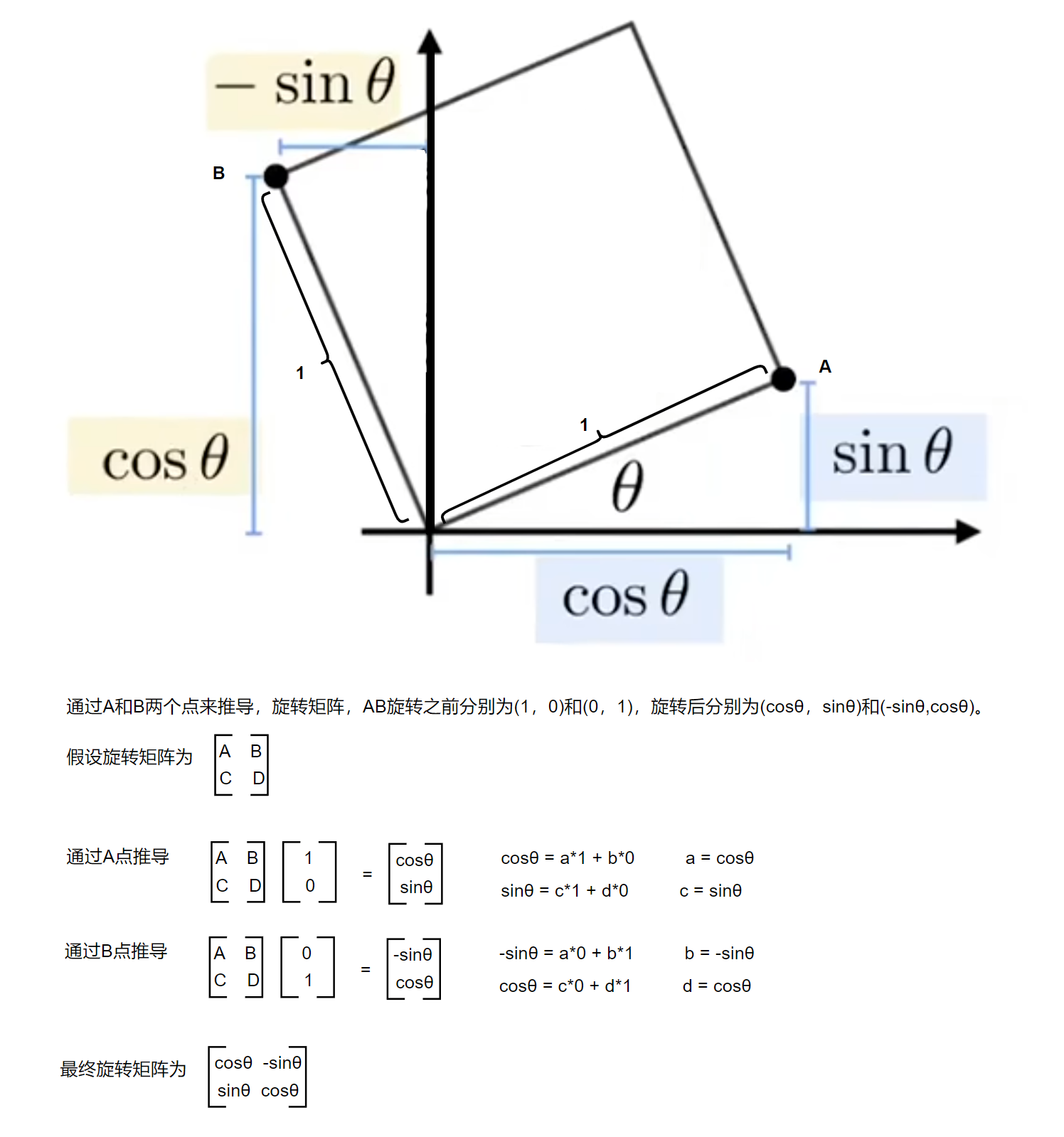
2D - Rotation Matrix 🔗
缩放矩阵推导
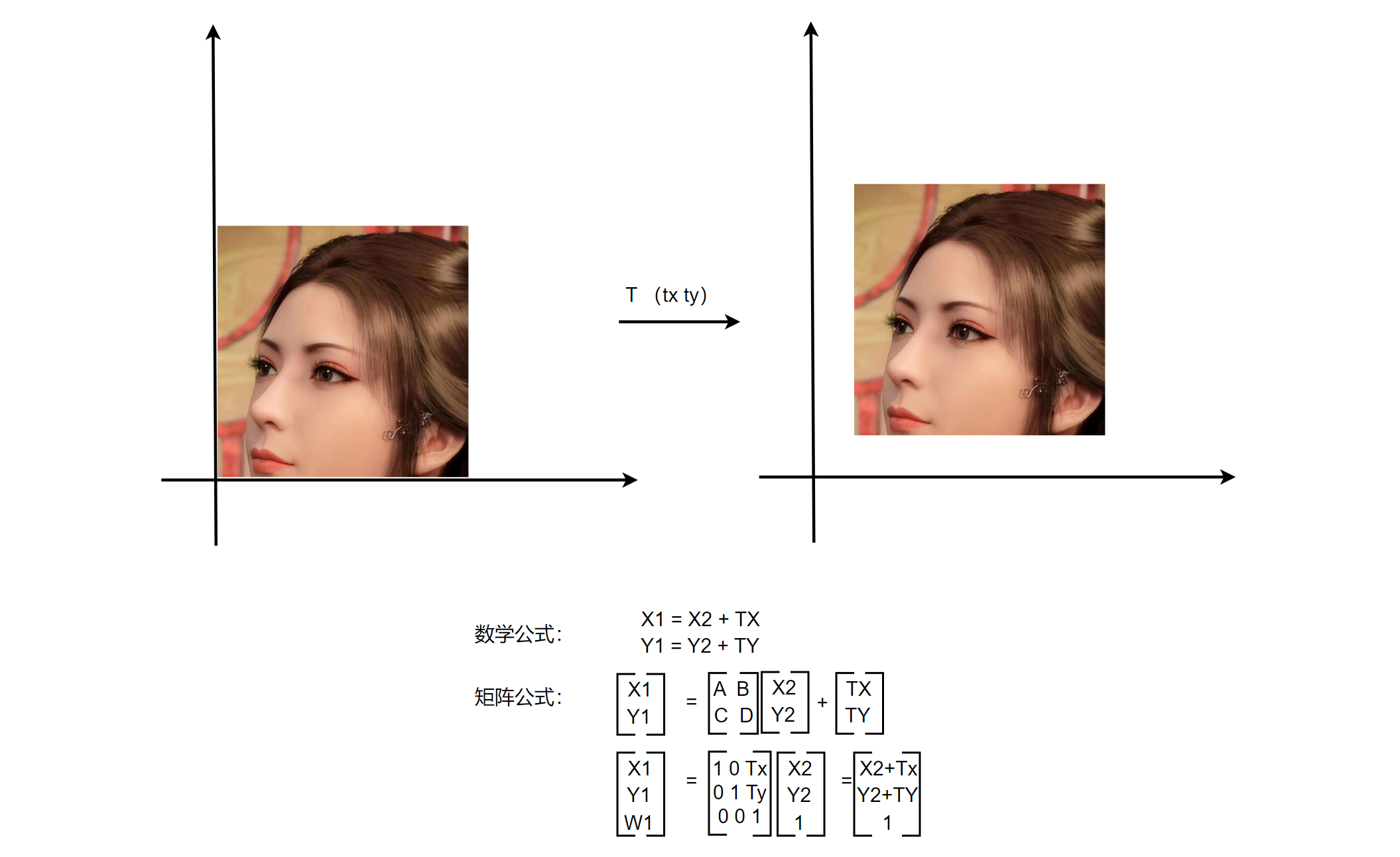
2D-Transiation Matrix 🔗
齐次坐标 🔗
齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示,是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。其主要用在一是区分向量和点;二是易于进行仿射变化(Affine Transformation) 。
齐次坐标中Ponit的(n+1)为1,Vector的(n+1)为0.
- Vector + Vector = Vector
- Point - Point = Vector
- Point + Vector = Point
一个2D点在齐次坐标系中的表示

齐次坐标系中的2D矩阵

3D Transformations 🔗

3D - Scale Matrix 🔗

3D - Transiation Matrix 🔗
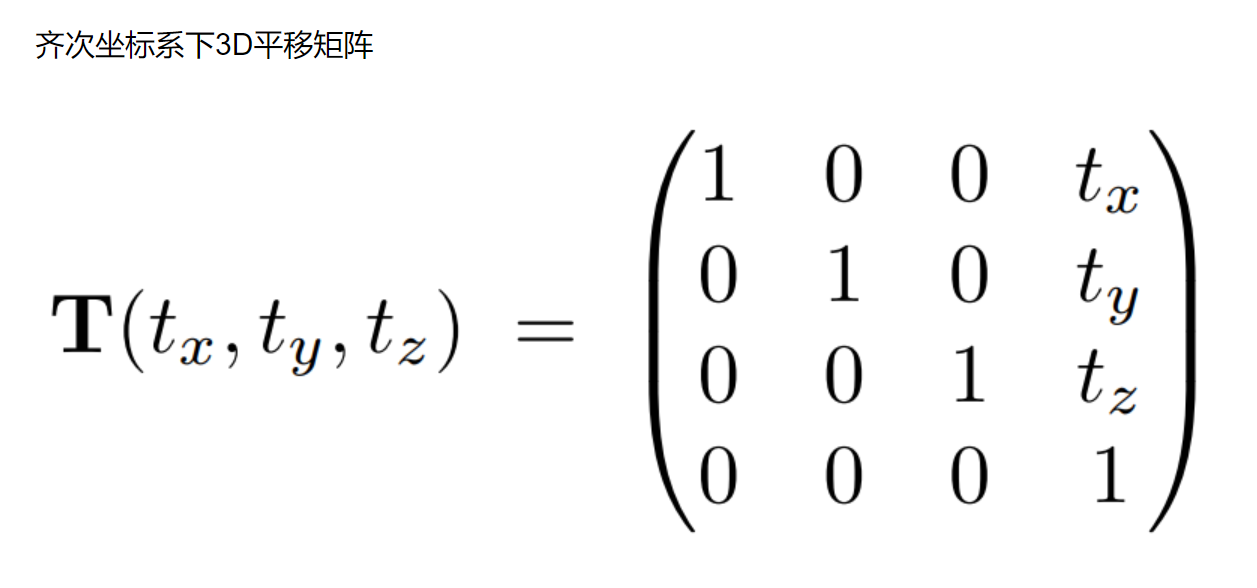
3D - Rotation Matrix 🔗
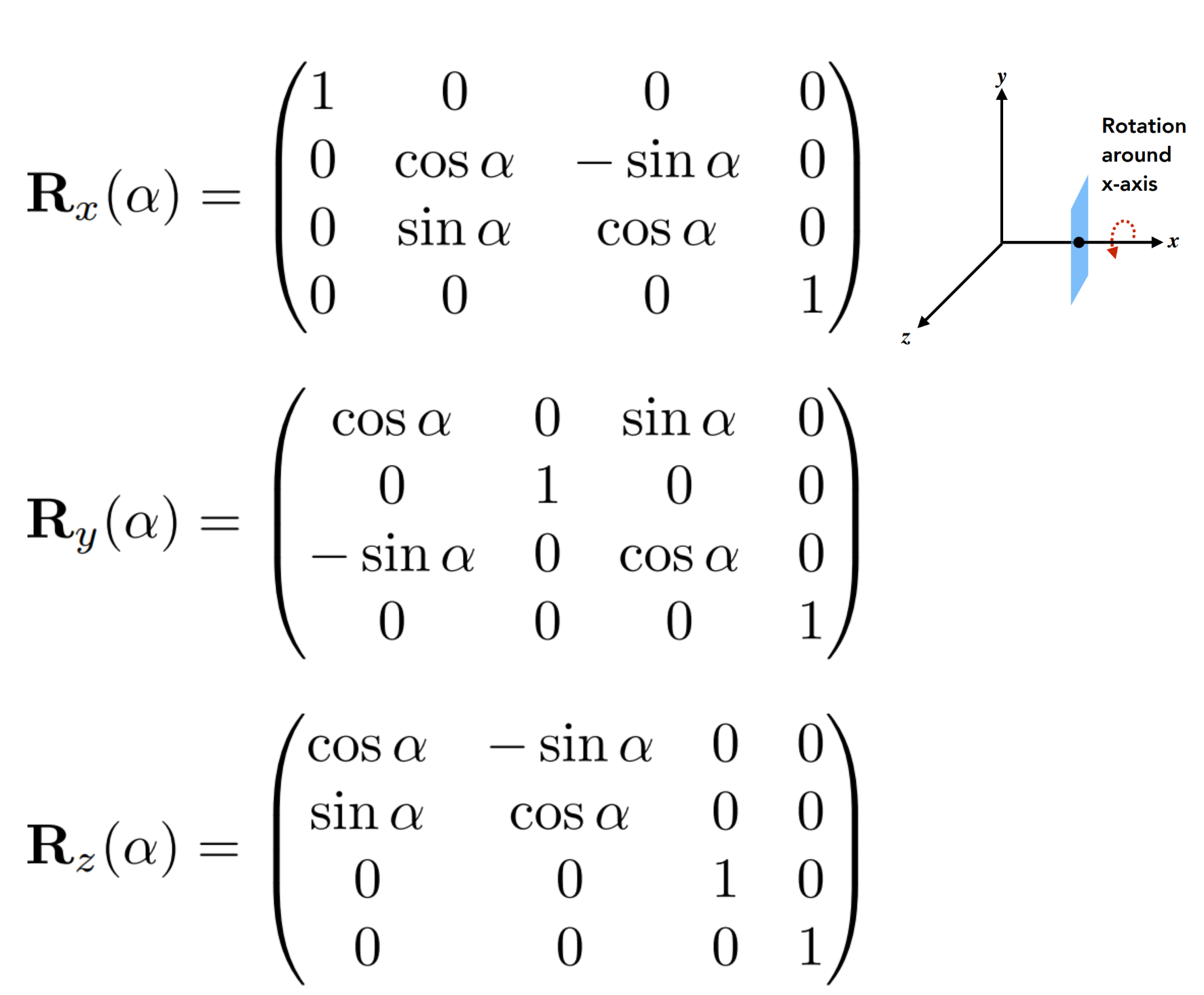
上面分别对应按照X,Y,Z轴进行旋转。
注意事项:
- 按照那个轴旋转,则该轴不动,旋转对应两个轴即可。
- 旋转矩阵的推导,遵循右手定责,进行叉乘计算得出。
欧拉角 🔗
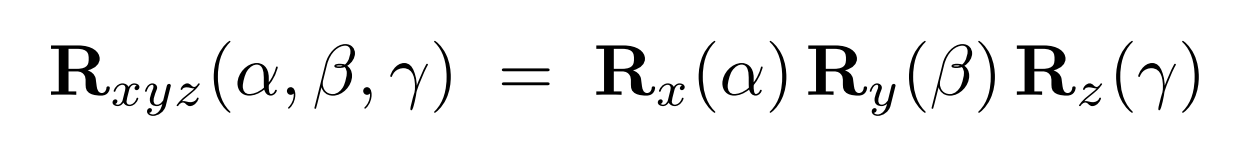
欧拉角计算公式分别按照α、β、γ进行旋转。
单位矩阵 🔗
单位矩阵从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0,任何矩阵与单位矩阵相乘都等于本身。
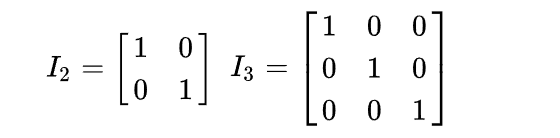
逆矩阵 🔗
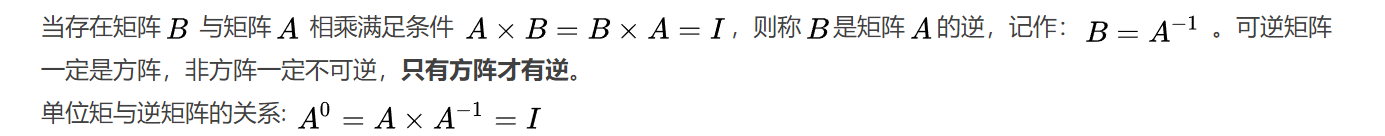
逆矩阵的意义在于变化之后的回退。当一个值通过一个矩阵运算后,如果想回退会原来的值,则使用逆矩阵进行计算即可。
你矩阵的推导:
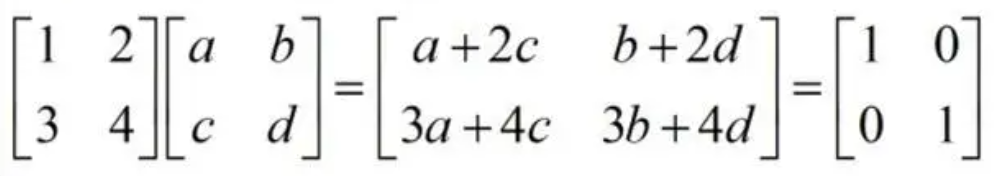
结论 🔗
搬砖愉快!